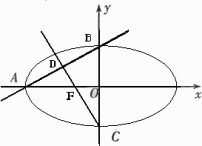
摘要： 如图.椭圆的离心率e=左焦点为F.A.B.C为其三个顶点.直线CF与AB交于D.则tan∠BDC的值等于 A． B． C． D． 联想:(1)设双曲线的一条准线与两条渐近线交于A.B两点.相应的焦点为F.若以AB为直径的圆恰好过F点.则离心率为 A． B． C．2 D． (2)双曲线的一条准线被它的两条渐近线截得线段的长度等于它的一个焦点到一条渐近线的距离.则双曲线的两条渐近线的夹角为 A．30° B．60° C．45° D．90°
网址：http://m.1010jiajiao.com/timu3_id_516796[举报]
(a＞b＞o)的离心率e＝
左焦点为F，A，B，C为其三个顶点，直线CF与AB交于D，则tan∠BDC的值等于
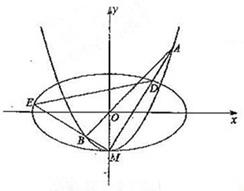如图，椭圆C1：| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
（Ⅰ）求C1，C2的方程；
（Ⅱ）设C2与y轴的交点为M，过坐标原点O的直线l与C2相交于点A、B，直线MA，MB分别与C1相交于D，E．
（i）证明：MD⊥ME；
（ii）记△MAB，△MDE的面积分别是S1，S2．问：是否存在直线l，使得
| S1 |
| S2 |
| 17 |
| 32 |
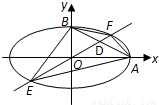
如图，椭圆的中心在坐标原点O，左右焦点分别为F1，F2，右顶点为A，上顶点为B，离心率
，三角形△BF1F2的周长为16．直线y=kx（k＞0）与AB相交于点D，与椭圆相交于E，F两点．
（1）求该椭圆的标准方程．
（2）求四边形AEBF面积的最大值．
查看习题详情和答案>>
，三角形△BF1F2的周长为16．直线y=kx（k＞0）与AB相交于点D，与椭圆相交于E，F两点．（1）求该椭圆的标准方程．
（2）求四边形AEBF面积的最大值．
查看习题详情和答案>>
=1（a＞b＞0）的离心率为
，x轴被曲线C2：y=x2-b截得的线段长等于C1的长半轴长．
=
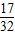？请说明理由．
=1（a＞b＞0）的离心率为
，x轴被曲线C2：y=x2-b截得的线段长等于C1的长半轴长．
=
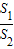？请说明理由．