摘要:6.A·P{an}中.an-1-a A.38 B.20 C.10 D.9 联想:(1)已知Sk表示数列{an}的前K项的和.且SK+1+SK=ak+1(KN),那么此数列是( ) A.递增数列 B.递减数列 C.常数列 D.摆动数列 (2)在G·P{an}中.对任意自然数n, 有a1+a2+-+an=2n-1,则a12+a22-+a ( ) A.4n-1 B. C. D.(2n-1)2 (3) .A·P{an}中,已知公差d=1, 前98项和S98=137,则a2+a4+-+a96+a98= (4) 数列{an}满足a1=,a1+a2+-+an=n2 ·an, 则数列{an}的通项公式为 . (5){an}.{bn}都是各项为正的数列.对任意的自然数n.都有an , b , an+1成等差数列.b , an+1.成等比数列. ①试问{bn}是否为A.P?为什么?②求证:对任意的自然数p.q, 成立,③如果a1 = 1 , b1 = , Sn = , 求
网址:http://m.1010jiajiao.com/timu3_id_516781[举报]
(2013•连云港一模)已知数列{an}中,a2=a(a为非零常数),其前n项和Sn满足:Sn=
(n∈N*)
(1)求数列{an}的通项公式;
(2)若a=2,且
am2-Sn=11,求m、n的值;
(3)是否存在实数a、b,使得对任意正整数p,数列{an}中满足an+b≤p的最大项恰为第3p-2项?若存在,分别求出a与b的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
| n(an-a1) |
| 2 |
(1)求数列{an}的通项公式;
(2)若a=2,且
| 1 |
| 4 |
(3)是否存在实数a、b,使得对任意正整数p,数列{an}中满足an+b≤p的最大项恰为第3p-2项?若存在,分别求出a与b的取值范围;若不存在,请说明理由.
下列选项中正确的是( )
A、若x>0且x≠1,则lnx+
| ||
| B、在数列{an}中,“|an+1|>an”是“数列{an}为递增数列”的必要非充分条件 | ||
| C、命题“所有素数都是奇数”的否定为“所有素数都是偶数” | ||
| D、若命题p为真命题,则其否命题为假命题 |
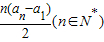
 am2-Sn=11,求m、n的值;
am2-Sn=11,求m、n的值;