摘要:设数列是单调递增的等差数列.前三项的和为12.前三项的积为48.则它的首项是( ) A.1 B.2 C.4 D.8 变式题1.在各项都为正数的等比数列中.首项.前三项和为21.则( ) 189 分析:本题主要是考查等比数列的基本概念和性质.可利用方程思想将等比数列问题转化为和处理.也可利用等比数列的定义进行求解. 解法一:设公比为.由题知.得或.∴.故选C. 解法二:由得.(舍去). .
网址:http://m.1010jiajiao.com/timu3_id_516736[举报]
设{an}是单调递增的等差数列,Sn为其前n项和,且满足4S3=S6,a2+2是a1,a13的等比中项.
(I)求数列{an}的通项公式;
(II)是否存在m,k∈N*,使am+am+4=ak+2?说明理由;
(Ⅲ)若数列{bn}满足bn=215-an,求数列{bn}的前n项积的最大值.
查看习题详情和答案>>
(I)求数列{an}的通项公式;
(II)是否存在m,k∈N*,使am+am+4=ak+2?说明理由;
(Ⅲ)若数列{bn}满足bn=215-an,求数列{bn}的前n项积的最大值.
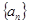 是单调递增的等差数列,前三项的和为12,前三项的积为48,则它的首项是
是单调递增的等差数列,前三项的和为12,前三项的积为48,则它的首项是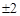 D.4
D.4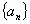 是单调递增的等差数列,前三项的和为12,前三项的积为48,则它的首项是
是单调递增的等差数列,前三项的和为12,前三项的积为48,则它的首项是