摘要：向量.向量的加法与减法.实数与向量的积.平面向量的坐标表示.线段的定比分点.平面向量的数量积.平面两点间的距离.平移.
网址：http://m.1010jiajiao.com/timu3_id_516537[举报]
材料：采访零向量
W：你好！零向量．我是《数学天地》的一名记者，为了让在校的高中生更好了解你，能不能对你进行一次采访呢？
零向量：当然可以，我们向量王国随时恭候大家的光临，很乐意接受你的采访，让高中生朋友更加了解我，更好地为他们服务．
W：好的，那就开始吧！你的名字有什么特殊的含义吗？
零向量：零向量就是长度为零的向量，它与数字0有着密切的联系，所以用0来表示我．
W：你与其他向量有什么共同之处呢？
零向量：既然我是向量王国的一个成员，就具有向量的基本性质，如既有大小又有方向，在进行加、减法运算时满足交换律和结合律，还定义了与实数的积．
W：你有哪些值得骄傲的特殊荣耀呢？
零向量：首先，我的方向是不定的，可以与任意的向量平行．其次，我还有其他一些向量所没有的特殊待遇：如我的相反向量仍是零向量；在向量的线性运算中，我与实数0很有相似之处．
W：你有如此多的荣耀，那么是否还有烦恼之事呢？
零向量：当然有了，在向量王国还有许多“权利和义务”却大有把我排斥在外之意，如平行向量的定义，向量共线定理，两向量夹角的定义都对我进行了限制．所有这些确实给一些高中生带来了很多苦恼，在此我向大家真诚地说一声：对不起，这不是我的错．但我还是很高兴有这次机会与大家见面．
W：OK！采访就到这里吧，非常感谢你的合作，再见！
零向量：Bye！
阅读上面的材料回答下面问题．
应用零向量时应注意哪些问题？
出于应用方便和数学交流的需要，我们教材定义向量的坐标如下：取
和
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量，根据平面向量基本定理，对于该平面上的任意一个向量
，则存在唯一的一对实数λ，μ，使得=
+μ，我们就把实数对（λ，μ）称作向量的坐标．并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式．现在我们用
和
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量，其中＜，＞=
，
（1）请你模仿直角坐标系xOy中向量坐标的定义方式，用向量和做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量的坐标；
（2）在（1）的基础上研究斜坐标系x‘Oy’中向量的加法、减法、数乘向量及数量积的坐标运算公式．
查看习题详情和答案>>
出于应用方便和数学交流的需要，我们教材定义向量的坐标如下：取
和
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量，根据平面向量基本定理，对于该平面上的任意一个向量
，则存在唯一的一对实数λ，μ，使得
=
+μ
，我们就把实数对（λ，μ）称作向量
的坐标．并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式．现在我们用
和
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量，其中＜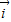
，
＞=
，
（1）请你模仿直角坐标系xOy中向量坐标的定义方式，用向量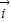
和
做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量
的坐标；
（2）在（1）的基础上研究斜坐标系x‘Oy’中向量的加法、减法、数乘向量及数量积的坐标运算公式．
查看习题详情和答案>>
和为直角坐标第xOy中与x轴和y轴正方向相同的单位向量，根据平面向量基本定理，对于该平面上的任意一个向量，则存在唯一的一对实数λ，μ，使得=+μ，我们就把实数对（λ，μ）称作向量的坐标．并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式．现在我们用和表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量，其中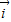＜，＞=，（1）请你模仿直角坐标系xOy中向量坐标的定义方式，用向量
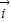和做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量的坐标；（2）在（1）的基础上研究斜坐标系x‘Oy’中向量的加法、减法、数乘向量及数量积的坐标运算公式．
查看习题详情和答案>>
出于应用方便和数学交流的需要，我们教材定义向量的坐标如下：取
和
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量，根据平面向量基本定理，对于该平面上的任意一个向量
，则存在唯一的一对实数λ，μ，使得
=λ
+μ
，我们就把实数对（λ，μ）称作向量
的坐标．并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式．现在我们用
和
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量，其中＜
，
＞=
，
（1）请你模仿直角坐标系xOy中向量坐标的定义方式，用向量
和
做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量
的坐标；
（2）在（1）的基础上研究斜坐标系x‘Oy’中向量的加法、减法、数乘向量及数量积的坐标运算公式． 查看习题详情和答案>>
| e1 |
| e2 |
| a |
| a |
| e1 |
| e2 |
| a |
| i |
| j |
| i |
| j |
| π |
| 3 |
（1）请你模仿直角坐标系xOy中向量坐标的定义方式，用向量
| i |
| j |
| a |
（2）在（1）的基础上研究斜坐标系x‘Oy’中向量的加法、减法、数乘向量及数量积的坐标运算公式． 查看习题详情和答案>>
出于应用方便和数学交流的需要，我们教材定义向量的坐标如下：取
和
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量，根据平面向量基本定理，对于该平面上的任意一个向量
，则存在唯一的一对实数λ，μ，使得
=λ
+μ
，我们就把实数对（λ，μ）称作向量
的坐标．并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式．现在我们用
和
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量，其中＜
，
＞=
，
（1）请你模仿直角坐标系xOy中向量坐标的定义方式，用向量
和
做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量
的坐标；
（2）在（1）的基础上研究斜坐标系x‘Oy’中向量的加法、减法、数乘向量及数量积的坐标运算公式．
查看习题详情和答案>>
| e1 |
| e2 |
| a |
| a |
| e1 |
| e2 |
| a |
| i |
| j |
| i |
| j |
| π |
| 3 |
（1）请你模仿直角坐标系xOy中向量坐标的定义方式，用向量
| i |
| j |
| a |
（2）在（1）的基础上研究斜坐标系x‘Oy’中向量的加法、减法、数乘向量及数量积的坐标运算公式．