摘要:设f(x)=ax2+bx+c.若f(1)=.问是否存在a.b.c∈R.使得不等式: x2+≤f(x)≤2x2+2x+对一切实数x都成立.证明你的结论. 解:由f(1)=得a+b+c=.令x2+=2x2+2x+x=-1.由f(x)≤2x2+2x+推得 f(-1)≤.由f(x)≥x2+推得f(-1)≥.∴f(-1)=.∴a-b+c=. 故2(a+c)=5.a+c=且b=1.∴f(x)=ax2+x+(-a).依题意:ax2+x+(-a)≥x2+ 对一切x∈R成立.∴a≠1且Δ=1-4(a-1)(2-a)≤0.得(2a-3)2≤0. ∴f(x)=x2+x+1易验证:x2+x+1≤2x2+2x+对x∈R都成立. ∴存在实数a=.b=1.c=1.使得不等式:x2+≤f(x)≤2x2+2x+对一切x∈R都成立.
网址:http://m.1010jiajiao.com/timu3_id_516467[举报]
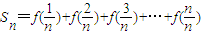 ,若不等式
,若不等式 对n∈N+恒成立,求实数m的取值范围;
对n∈N+恒成立,求实数m的取值范围;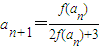 ;b1=1,
;b1=1,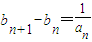 ,记
,记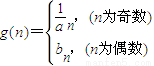 ,问是否存在k∈N,使g(k+1)=2g(k)成立,若存在,求出k值;若不存在,说明理由.
,问是否存在k∈N,使g(k+1)=2g(k)成立,若存在,求出k值;若不存在,说明理由.