摘要：已知实数a>0.函数f(x)=ax(x-2)2(x∈R)有极大值32. (1)求实数a的值, (2)求函数f(x)的单调区间. 解:(1)∵f(x)=ax(x-2)2=ax3-4ax2+4ax. ∴(x)=3ax2-8ax+4a. 由(x)=0.得3ax2-8ax+4a=0. ∵a≠0.∴3x2-8x+4=0. 解得x=2或x=. ∵a>0.∴x<或x>2时.(x)>0, <x<2时.(x)<0. ∴当x=时.f(x)有极大值32.即 a-a+a=32.∴a=27. (2)f(x)在(-∞.)和上是增函数.在(.2)上是减函数.
网址：http://m.1010jiajiao.com/timu3_id_516178[举报]
（
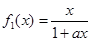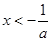）与曲线
（
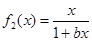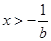）上任意两点，则|
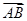|最小值为 . 
（
）与曲线
（
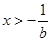）上任意两点，则|
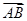|最小值为 . 
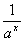，则下列选项正确的是
(a>0).方程
有两个实根
.
,函数
图象的对称轴是直线
,求证
;
,且
满足
>0，且
，则xy取值的范围是( )
B．
C．
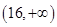D．