摘要:(2005年北京西城区模拟题)如果函数y=f(x)的导函数的图象如图所示.给出下列判断: ①函数y=f(x)在区间(-3.-)内单调递增, ②函数y=f(x)在区间(-.3)内单调递减, ③函数y=f(x)在区间(4.5)内单调递增, ④当x=2时.函数y=f(x)有极小值, ⑤当x=-时.函数y=f(x)有极大值. 则上述判断中正确的是 . 答案:③
网址:http://m.1010jiajiao.com/timu3_id_516174[举报]
 已知函数f(x)的定义域为[-1,5],部分对应值如下表. 已知函数f(x)的定义域为[-1,5],部分对应值如下表.
①函数f(x)在[0,1]上是减函数; ②如果当x∈[-1,t]时,f(x)最大值是2,那么t的最大值为4; ③函数y=f(x)-a有4个零点,则1≤a<2; ④若f(x)在[-1,5]上的极小值为-2,且 y=t与f(x)有两个交点,则-2<t<1. 其中真命题的个数是( ) |
查看习题详情和答案>>
(2012•天津模拟)已知函数f(x)的定义域为[-1,5],部分对应值如下表.
f(x)的导函数y=f′(x)的图象如图所示:
下列关于f(x)的命题:
①函数f(x)是周期函数;
②函数f(x)在[0,2]是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点;
⑤函数y=f(x)-a的零点个数可能为0、1、2、3、4个.
其中正确命题的序号是
查看习题详情和答案>>
| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
下列关于f(x)的命题:

①函数f(x)是周期函数;
②函数f(x)在[0,2]是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点;
⑤函数y=f(x)-a的零点个数可能为0、1、2、3、4个.
其中正确命题的序号是
②⑤
②⑤
.记定义在R上的函数y=f(x)的导函数为f′(x).如果存在x0∈[a,b],使得f(b)-f(a)=f′(x0)(b-a)成立,则称x0为函数f(x)在区间[a,b]上的“中值点”.那么函数f(x)=x3-3x在区间[-2,2]上的“中值点”为 .
查看习题详情和答案>>
 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题: 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题:
②函数f(x)在[0,1]是减函数,在[1,2]是增函数; ③当1<a<2时,函数y=f(x)-a有4个零点; ④如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最小值为0, 其中所有正确命题的个数是( ) |
查看习题详情和答案>>
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示. 下列关于f(x)的命题:
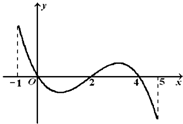 ②函数f(x)在[0,2]上是减函数; ③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4; ④当1<a<2时,函数y=f(x)-a有4个零点; ⑤函数y=f(x)-a的零点个数可能为0、1、2、3、4个. 其中正确命题的个数是( ) |
查看习题详情和答案>>