摘要：15．已知为正数.且满足.则的最大值是 .
网址：http://m.1010jiajiao.com/timu3_id_516114[举报]
已知f（x），g（x）都是定义在R上的函数，g（x）≠0，f′（x）g（x）＞f（x）g′（x），f（x）=ax•g（x）（a＞0，且a≠1），
+
=
，在有穷数列
（n=1，2，…10）中，任意取正整数k（1≤k≤10） 且满足前k项和大于126，则k的最小值为（ ）
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
| f(n) |
| g(n) |
| A、6 | B、7 | C、8 | D、9 |
已知函数f（x）的定义域为[0，1]，且同时满足：①f（1）=3；②f（x）≥2对一切x∈[0，1]恒成立；③若x1≥0，x2≥0，x1+x2≤1，则f（x1+x2）≥f（x1）+f（x2）-2，
（Ⅰ）求函数f（x）的最大值和最小值；
（Ⅱ）试比较f(
)与
+2的大小；
（Ⅲ）某同学发现：当x=
（n∈N）时，有f（x）＜2x+2，由此他提出猜想：对一切x∈（0，1]，都有f（x）＜2x+2，请你判断此猜想是否正确，并说明理由．
查看习题详情和答案>>
（Ⅰ）求函数f（x）的最大值和最小值；
（Ⅱ）试比较f(
| 1 |
| 2n |
| 1 |
| 2n |
（Ⅲ）某同学发现：当x=
| 1 |
| 2n |
已知一非零向量数列{an}满足a1=（1，1）an=(xn，yn)=
(xn-1-yn-1，xn-1+yn-1)（n≥2且n∈N*）．给出以下结论：
①数列{|an|}是等差数列，②|a1|•|a5|=
；③设cn=2log2|an|，则数列{cn}的前n项和为Tn，当且仅当n=2时，Tn取得最大值；④记向量an与an-1的夹角为θn（n≥2），均有θn=
．其中所有正确结论的序号是 ．
查看习题详情和答案>>
| 1 |
| 2 |
①数列{|an|}是等差数列，②|a1|•|a5|=
| 1 |
| 2 |
| π |
| 4 |
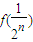与
的大小；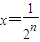
（n∈N）时，有f（x）＜2x+2，由此他提出猜想：对一切x∈（0，1]，都有f（x）＜2x+2，请你判断此猜想是否正确，并说明理由．
与
的大小；
（n∈N）时，有f（x）＜2x+2，由此他提出猜想：对一切x∈（0，1]，都有f（x）＜2x+2，请你判断此猜想是否正确，并说明理由．