摘要:对于函数与方程.课标:对任一函数的零点进行研究.方法基本.简单.易于掌握,课标:求近似解可以无限精确.大纲:画图观察出方程的解的近似值如求方程的近似解. ①设函数与的图象的交点为. 则所在的区间是( ) A. B. C. D. ②已知是实数.函数.如果函数在区间上有零点.求的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_515807[举报]
(本小题满分14分)设函数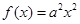 (
(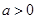 ),
), .
.
(Ⅰ)令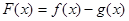 ,讨论
,讨论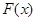 的单调性;
的单调性;
(Ⅱ)关于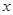 的不等式
的不等式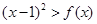 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数 的取值范围;
的取值范围;
(Ⅲ)对于函数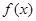 与
与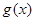 定义域上的任意实数
定义域上的任意实数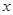 ,若存在常数
,若存在常数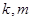 ,使得
,使得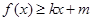 和
和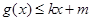 都成立,则称直线
都成立,则称直线 为函数
为函数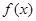 与
与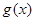 的“分界线”.设
的“分界线”.设 ,
,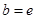 ,试探究
,试探究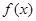 与
与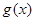 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
查看习题详情和答案>>
(本小题满分14分)
已知:函数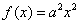 (
(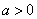 ),
),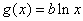 .
.
(1)若函数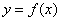 图象上的点到直线
图象上的点到直线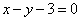 距离的最小值为
距离的最小值为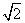 ,求
,求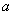 的值;
的值;
(2)关于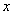 的不等式
的不等式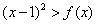 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数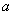 的取值范围;
的取值范围;
(3)对于函数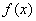 与
与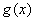 定义域上的任意实数
定义域上的任意实数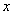 ,若存在常数
,若存在常数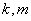 ,使得不等式
,使得不等式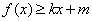 和
和 都成立,则称直线
都成立,则称直线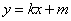 为函数
为函数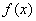 与
与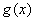 的“分界线”。设
的“分界线”。设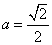 ,
,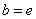 ,试探究
,试探究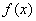 与
与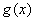 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
查看习题详情和答案>>
、对于函数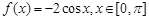 与函数
与函数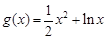 有下列命题:
有下列命题:
①无论函数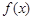 的图像通过怎样的平移所得的图像对应的函数都不会是奇函数;
的图像通过怎样的平移所得的图像对应的函数都不会是奇函数;
②函数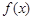 的图像与两坐标轴及其直线
的图像与两坐标轴及其直线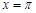 所围成的封闭图形的面积为4;
所围成的封闭图形的面积为4;
③方程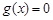 有两个根;
有两个根;
④函数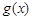 图像上存在一点处的切线斜率小于0;
图像上存在一点处的切线斜率小于0;
⑤若函数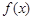 在点P处的切线平行于函数
在点P处的切线平行于函数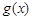 在点Q处的切线,则直线PQ的斜率为
在点Q处的切线,则直线PQ的斜率为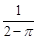 ,其中正确的命题是________.(把所有正确命题的序号都填上)
,其中正确的命题是________.(把所有正确命题的序号都填上)
查看习题详情和答案>>
 (
(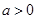 ),
), .
. 图象向右平移一个单位即可得到函数
图象向右平移一个单位即可得到函数 的图象,试写出
的图象,试写出 的不等式
的不等式 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数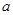 的取值范围;
的取值范围; 与
与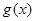 定义域上的任意实数
定义域上的任意实数 ,使得
,使得 和
和 都成立,则称直线
都成立,则称直线 为函数
为函数 ,
, ,试探究
,试探究 (
( ),
), .
.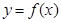 图象向右平移一个单位即可得到函数
图象向右平移一个单位即可得到函数 的图象,试写出
的图象,试写出 的不等式
的不等式 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数 的取值范围;
的取值范围; 与
与 定义域上的任意实数
定义域上的任意实数 ,使得
,使得 和
和 都成立,则称直线
都成立,则称直线 为函数
为函数 ,
,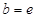 ,试探究
,试探究