摘要：证明三角不等式的方法:比较法.配方法.反证法.分析法.利用函数的单调性.利用正.余弦函数的有界性.利用单位圆三角函数线及判别法等.
网址：http://m.1010jiajiao.com/timu3_id_515700[举报]
阅读不等式5x≥4x+1的解法：
解：由5x≥4x+1，两边同除以5x可得1≥(
)x+(
)x．
由于0＜
＜
＜1，显然函数f（x）=（
）x+（
）x在R上为单调减函数，
而f(1)=
+
=1，故当x＞1时，有f（x）=（
）x+（
）x＜f（x）=1
所以不等式的解集为{x|x≥1}．
利用解此不等式的方法解决以下问题：
（1）解不等式：9x＞5x+4x；
（2）证明：方程5x+12x=13x有唯一解，并求出该解．
查看习题详情和答案>>
解：由5x≥4x+1，两边同除以5x可得1≥(
| 4 |
| 5 |
| 1 |
| 5 |
由于0＜
| 1 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
而f(1)=
| 4 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
所以不等式的解集为{x|x≥1}．
利用解此不等式的方法解决以下问题：
（1）解不等式：9x＞5x+4x；
（2）证明：方程5x+12x=13x有唯一解，并求出该解．
比较法证明不等式可分为作差比较法和作商比较法：
(1)要证明a＞b，只要证明________；要证a＜b，只要证明________．这种证明不等式的方法，叫做作差比较法；
(2)要证明a＞b(b＞0)，只要证明________；要证b＞a(a＞0)，只要证明________．这种证明不等式的方法，叫做作商比较法．
查看习题详情和答案>>利用某些已经证明的不等式，从________出发，运用不等式的________推出所要证的不等式，这种证明不等式的方法叫做综合法．其思维特点是________，即从________逐步向________靠拢．
查看习题详情和答案>>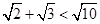
”可选择的方法有以下几种，其中最合理的是 。（填序号）