摘要：1．熟练掌握三角变换的所有公式.理解每个公式的意义.应用特点.常规使用方法等,熟悉三角变换常用的方法--化弦法.降幂法.角的变换法等,并能应用这些方法进行三角函数式的求值.化简.证明,掌握三角变换公式在三角形中应用的特点.并能结合三角形的公式解决一些实际问题．
网址：http://m.1010jiajiao.com/timu3_id_515695[举报]
若函数f（x）具有性质：f(
)=-f(x)，则称f（x）是满足“倒负”变换的函数．下列四个函数：
①f（x）=logax（a＞0且a≠1）；
②f（x）=ax（a＞0且a≠1）；
③y=x-
；
④f(x)=
．
其中，满足“倒负”变换的所有函数的序号是
查看习题详情和答案>>
| 1 |
| x |
①f（x）=logax（a＞0且a≠1）；
②f（x）=ax（a＞0且a≠1）；
③y=x-
| 1 |
| x |
④f(x)=
|
其中，满足“倒负”变换的所有函数的序号是
①③④
①③④
．若函数f（x）具有性质：f(
)=-f(x)，则称f（x）是满足“倒负”变换的函数．下列四个函数：
①f（x）=logax（a＞0且a≠1）；
②f（x）=ax（a＞0且a≠1）；
③y=x-
；
④f(x)=
．
其中，满足“倒负”变换的所有函数的序号是______．
查看习题详情和答案>>
| 1 |
| x |
①f（x）=logax（a＞0且a≠1）；
②f（x）=ax（a＞0且a≠1）；
③y=x-
| 1 |
| x |
④f(x)=
|
其中，满足“倒负”变换的所有函数的序号是______．
若函数f（x）具有性质：
，则称f（x）是满足“倒负”变换的函数．下列四个函数：
①f（x）=logax（a＞0且a≠1）；
②f（x）=ax（a＞0且a≠1）；
③
；
④
．
其中，满足“倒负”变换的所有函数的序号是 ． 查看习题详情和答案>>
，则称f（x）是满足“倒负”变换的函数．下列四个函数：①f（x）=logax（a＞0且a≠1）；
②f（x）=ax（a＞0且a≠1）；
③
； ④
．其中，满足“倒负”变换的所有函数的序号是 ． 查看习题详情和答案>>
，则称f(x)是满足“倒负”变换的函数．下列四个函数：
；
．
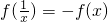，则称f（x）是满足“倒负”变换的函数．下列四个函数：
； 
．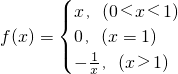