摘要:函数思想.是指用函数的概念和性质去分析问题.转化问题和解决问题.方程思想.是从问题的数量关系入手.运用数学语言将问题中的条件转化为数学模型(方程.不等式.或方程与不等式的混合组).然后通过解方程来使问题获解.有时.还实现函数与方程的互相转化.接轨.达到解决问题的目的. Ⅰ.再现性题组:1. 方程lgx+x=3的解所在的区间为 . A. C.
网址:http://m.1010jiajiao.com/timu3_id_515242[举报]
设函数f(x)=x3-3ax+b(a≠0),且曲线y=f(x)在点(2,f(x))处与直线y=8相切.
(Ⅰ)求a,b的值;
(Ⅱ)求函数f(x)的单调区间与极值点.
提示:导数的几何意义是指:函数在该点的导数值等于与曲线相切于该点的切线的斜率k=f/(x)
.
查看习题详情和答案>>
(Ⅰ)求a,b的值;
(Ⅱ)求函数f(x)的单调区间与极值点.
提示:导数的几何意义是指:函数在该点的导数值等于与曲线相切于该点的切线的斜率k=f/(x)
|
(2003•东城区二模)某城市为了改善交通状况,需进行路网改造.已知原有道路a个标段(注:1个标段是指一定长度的机动车道),拟增建x个标段的新路和n个道路交叉口,n与x满足关系n=ax+b,其中b为常数.设新建1个标段道路的平均造价为k万元,新建1个道路交叉口的平均造价是新建1个标段道路的平均造价的β倍(β≥1),n越大,路网越通畅,记路网的堵塞率为μ,它与β的关系为μ=
.
(Ⅰ)写出新建道路交叉口的总造价y(万元)与x的函数关系式:
(Ⅱ)若要求路网的堵塞率介于5%与10%之间,而且新增道路标段为原有道路标段数的25%,求新建的x个标段的总造价与新建道路交叉口的总造价之比P的取值范围;
(Ⅲ)当b=4时,在(Ⅱ)的假设下,要使路网最通畅,且造价比P最高时,问原有道路标段为多少个?
查看习题详情和答案>>
| 1 | 2(1+β) |
(Ⅰ)写出新建道路交叉口的总造价y(万元)与x的函数关系式:
(Ⅱ)若要求路网的堵塞率介于5%与10%之间,而且新增道路标段为原有道路标段数的25%,求新建的x个标段的总造价与新建道路交叉口的总造价之比P的取值范围;
(Ⅲ)当b=4时,在(Ⅱ)的假设下,要使路网最通畅,且造价比P最高时,问原有道路标段为多少个?
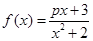 (其中
(其中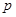 为常数,
为常数,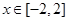 )为偶函数.
)为偶函数. 在
在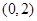 上是单调减函数;
上是单调减函数;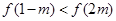 ,求实数
,求实数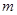 的取值范围.
的取值范围. ,其中
,其中 是常数,其图像是一条直线,称这个函数为线性函数,而对于非线性可导函数
是常数,其图像是一条直线,称这个函数为线性函数,而对于非线性可导函数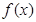 ,在已知点
,在已知点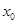 附近一点
附近一点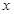 的函数值
的函数值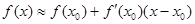 ,利用这一方法,对于实数
,利用这一方法,对于实数 ,取
,取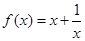 .
.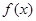 在
在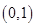 上是减函数;
上是减函数;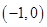 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).