摘要: 已知方程x+(a-2)x+a-1=0的两根x.x.则点P(x,x)在圆x+y=4上.则实数a= . Ⅱ.示范性题组: 例1. 已知长方体的全面积为11.其12条棱的长度之和为24.则这个长方体的一条对角线长为 . A. 2 B. C. 5 D. 6 [分析] 先转换为数学表达式:设长方体长宽高分别为x,y,z.则 ,而欲求对角线长.将其配凑成两已知式的组合形式可得. [解]=- 例2. 设方程x+kx+2=0的两根为p.q.若()+()≤7成立.求k的取值范围. [解] 由韦达定理得:p+q=-k.pq=2 , ()+()====≤7. 解得k≤-或k≥ . 又 ∵p.q为方程两实根. ∴ Δ=k-8≥0 ∴k的取值范围是:-≤k≤- 或者 ≤k≤ [注] 实系数一元二次方程问题.注意Δ.恰当运用韦达定理,由已知的不等式联想到配方.表示成p+q与pq的组合式. 例3. 设非零复数a.b满足a+ab+b=0.求()+() . [分析] 对已知式可以联想:变形为()+()+1=0.则=ω ,或配方为(a+b)=ab .则代入所求式即得. [解] [注] 配方.简化表达式,巧用1的立方虚根.计算高次幂,活用ω的性质. [另解] 解出=-后.用三角形式完成后面的运算: Ⅲ.巩固性题组:
网址:http://m.1010jiajiao.com/timu3_id_515196[举报]
已知方程x2+(1+a)x+1+a+b=0的两个实根x1,x2,满足0<x1<1<x2,则
的取值范围是( )
| b |
| a |
| A、(-2,0) | ||
B、(0,
| ||
C、(-2,-
| ||
D、(-
|
 )
) 的取值范围是( )
的取值范围是( ) )
)
 ,0)
,0)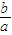 的取值范围是( )
的取值范围是( ) )
)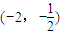
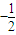 ,0)
,0)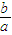 的取值范围是( )
的取值范围是( ) )
)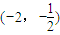
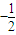 ,0)
,0)