摘要：11．已知{an}为递增数列.且对于任意正整数n.an=-n2+λn恒成立.则λ的取值范围是 答案:λ>3 点评:利用二次函数单调性讨论较繁.且易错.利用an+1>an恒成立较方便.
网址：http://m.1010jiajiao.com/timu3_id_514914[举报]
已知{an}为递增的等比数列，且{a1，a3，a5}?{-10，-6，-2，0，1，3，4，16}．
（I）求数列{an}的通项公式；
（II）是否存在等差数列{bn}，使得a1bn+a2bn-1+a3bn-2+…+anb1=2n+1-n-2对一切n∈N*都成立？若存在，求出bn；若不存在，说明理由． 查看习题详情和答案>>
（I）求数列{an}的通项公式；
（II）是否存在等差数列{bn}，使得a1bn+a2bn-1+a3bn-2+…+anb1=2n+1-n-2对一切n∈N*都成立？若存在，求出bn；若不存在，说明理由． 查看习题详情和答案>>
已知{an}是递增数列，其前n项和为Sn，a1＞1，且10Sn=（2an+1）（an+2），n∈N*．
（Ⅰ）求数列{an}的通项an；
（Ⅱ）是否存在m，n，k∈N*，使得2（am+an）=ak成立？若存在，写出一组符合条件的m，n，k的值；若不存在，请说明理由；
（Ⅲ）设bn=an-
，cn=
，若对于任意的n∈N*，不等式
-
≤0恒成立，求正整数m的最大值．
查看习题详情和答案>>
（Ⅰ）求数列{an}的通项an；
（Ⅱ）是否存在m，n，k∈N*，使得2（am+an）=ak成立？若存在，写出一组符合条件的m，n，k的值；若不存在，请说明理由；
（Ⅲ）设bn=an-
| n-3 |
| 2 |
| 2(n+3)an |
| 5n-1 |
| ||||||
31(1+
|
| 1 | ||
|
已知{an}是递增数列，其前n项和为Sn，a1＞1，且10Sn=（2an+1）（an+2），n∈N+．
（Ⅰ）求数列{an}的通项an；
（Ⅱ）设bn=an-
，若对于任意的n∈N+．，不等式
≤(1+
)(1+
)…(1+
)-
恒成立，求正整数m的最大值．
查看习题详情和答案>>
（Ⅰ）求数列{an}的通项an；
（Ⅱ）设bn=an-
| n-3 |
| 2 |
| ||
| 31 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 1 | ||
|
{－10，－6，－2,0,1,3,4,16}．
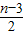，cn=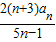
，若对于任意的n∈N*，不等式
-
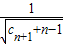≤0恒成立，求正整数m的最大值．