摘要:11.在边长为a的正三角形中.点P.Q.R分别在BC.CA.AB上.且BP+CQ+AR=a,设BP=x,CQ=y,AR=z,三角形PQR的面积为s,求s的最大值及相应的x.y.z的值. 解 设ΔBPR.ΔPCR.ΔARQ的面积为s1..s2.s3.则 S=SΔABC-S1-S2-S3=a2-[a2-]= 由x+y+z=a,得xy+yz+zx≤,∴Smav=a2.此时.x=y=z= 错因:不知如何使用基本不等式.
网址:http://m.1010jiajiao.com/timu3_id_514738[举报]
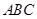 中,
中, ,
,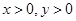 ,且
,且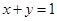 ,则
,则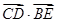 的最大值为( )
的最大值为( ) B.
B.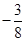 C.
C.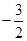 D.
D.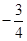
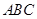 中,
中,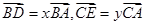 ,
,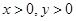 ,且
,且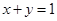 ,则
,则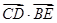 的最大值为( )
的最大值为( )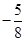 B.
B.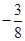 C.
C.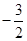 D.
D.