网址:http://m.1010jiajiao.com/timu3_id_513323[举报]
对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(Ⅰ)证明:对任意的x1,x2∈(0,1),x1<x2,若f(x1)≥f(x2),则(0,x2)为含峰区间;若f(x1)≤f(x2),则(x1,1)为含峰区间;
(Ⅱ)对给定的r(0<r<0.5),证明:存在x1,x2∈(0,1),满足x2-x1≥2r,使得由(Ⅰ)确定的含峰区间的长度不大于0.5+r;
(Ⅲ)选取x1,x2∈(0,1),x1<x2由(Ⅰ)可确定含峰区间为(0,x2)或(x1,1),在所得的含峰区间内选取x3,由x3与x1或x3与x2类似地可确定是一个新的含峰区间.在第一次确定的含峰区间为(0,x2)的情况下,试确定x1,x2,x3的值,满足两两之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34.
(区间长度等于区间的右端点与左端点之差). 查看习题详情和答案>>
设f(x)是定义在[0,1]上的函数,若存在x*∈(0,1),使得f(x)在[0,x*]上单调递增,在[x*,1]上单调递减,则称f(x)为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(I)证明:对任意的 ∈(O,1),
∈(O,1), ,若f(
,若f( )≥f(
)≥f(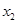 ),则(0,
),则(0,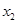 )为含峰区间:若f(
)为含峰区间:若f( )
) f(
f(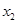 ),则
),则 为含峰区间:
为含峰区间:
(II)对给定的r(0<r<0.5),证明:存在 ∈(0,1),满足
∈(0,1),满足 ,使得由(I)所确定的含峰区间的长度不大于0.5+r:
,使得由(I)所确定的含峰区间的长度不大于0.5+r:
(III)选取 ∈(O,1),,由(I)可确定含峰区间为
∈(O,1),,由(I)可确定含峰区间为 或
或 ,在所得的含峰区间内选取
,在所得的含峰区间内选取 ,由
,由 与
与 或
或 与
与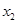 类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,
类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,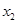 )的情况下,试确定的值
)的情况下,试确定的值 ,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
查看习题详情和答案>>
(05年北京卷理)(14分)
设![]() 是定义在[0,1]上的函数,若存在
是定义在[0,1]上的函数,若存在![]() ,使得
,使得![]() 在[0,
在[0,![]() ]上单调递增,在[
]上单调递增,在[![]() ,1]单调递减,则称
,1]单调递减,则称![]() 为[0,1]上的单峰函数,
为[0,1]上的单峰函数,![]() 为峰点,包含峰点的区间为含峰区间
为峰点,包含峰点的区间为含峰区间![]() 对任意的[0,1]上的单峰函数
对任意的[0,1]上的单峰函数![]() ,下面研究缩短其含峰区间长度的方法
,下面研究缩短其含峰区间长度的方法![]()
(Ⅰ)证明:对任意的![]()
![]() ,
, ![]() ,若
,若![]() ,则(0,
,则(0,![]() )为含峰区间;若
)为含峰区间;若![]() ,则(
,则(![]() ,1)为含峰区间;
,1)为含峰区间;
(Ⅱ)对给定的![]() (0<
(0<![]() <0.5),证明:存在
<0.5),证明:存在![]()
![]() ,满足
,满足![]() ,使得由(Ⅰ)确定的含峰区间的长度不大于0.5+
,使得由(Ⅰ)确定的含峰区间的长度不大于0.5+![]() ;
;
(Ⅲ)选取![]()
![]() ,
,![]() 由(Ⅰ)可确定含峰区间为(0,
由(Ⅰ)可确定含峰区间为(0,![]() )或(
)或(![]() ,1),在所得的含峰区间内选取
,1),在所得的含峰区间内选取![]() ,由
,由![]() 与
与![]() 或
或![]() 与
与![]() 类似地可确定是一个新的含峰区间.在第一次确定的含峰区间为(0,
类似地可确定是一个新的含峰区间.在第一次确定的含峰区间为(0,![]() )的情况下,试确定
)的情况下,试确定![]() 的值,满足两两之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34
的值,满足两两之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34![]()
(区间长度等于区间的右端点与左端点之差)![]()
对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(Ⅰ)证明:对任意的x1,x2∈(0,1),x1<x2,若f(x1)≥f(x2),则(0,x2)为含峰区间;若f(x1)≤f(x2),则(x1,1)为含峰区间;
(Ⅱ)对给定的r(0<r<0.5),证明:存在x1,x2∈(0,1),满足x2-x1≥2r,使得由(Ⅰ)确定的含峰区间的长度不大于0.5+r;
(Ⅲ)选取x1,x2∈(0,1),x1<x2由(Ⅰ)可确定含峰区间为(0,x2)或(x1,1),在所得的含峰区间内选取x3,由x3与x1或x3与x2类似地可确定是一个新的含峰区间.在第一次确定的含峰区间为(0,x2)的情况下,试确定x1,x2,x3的值,满足两两之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34.
(区间长度等于区间的右端点与左端点之差).
查看习题详情和答案>>
对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(Ⅰ)证明:对任意的x1,x2∈(0,1),x1<x2,若f(x1)≥f(x2),则(0,x2)为含峰区间;若f(x1)≤f(x2),则(x1,1)为含峰区间;
(Ⅱ)对给定的r(0<r<0.5),证明:存在x1,x2∈(0,1),满足x2-x1≥2r,使得由(Ⅰ)确定的含峰区间的长度不大于0.5+r;
(Ⅲ)选取x1,x2∈(0,1),x1<x2由(Ⅰ)可确定含峰区间为(0,x2)或(x1,1),在所得的含峰区间内选取x3,由x3与x1或x3与x2类似地可确定是一个新的含峰区间.在第一次确定的含峰区间为(0,x2)的情况下,试确定x1,x2,x3的值,满足两两之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34.
(区间长度等于区间的右端点与左端点之差).
查看习题详情和答案>>