摘要:19. 如图.在四棱锥中.侧棱PA⊥底面ABCD. AD∥BC.∠ABC=... (Ⅰ) 求点D到平面PBC的距离, (Ⅱ) 求二面角的大小. 解:(Ⅰ)如图.在四棱锥中. ∵BC∥AD.从而点D到平面PBC间的距离等于点A到平面PBC的距离. ∵∠ABC=.∴AB⊥BC. 又PA⊥底面ABCD.∴PA⊥BC. ∴BC⊥平面 PAB.------2分 ∴平面PAB⊥平面PBC.交线为PB.过A作AE⊥PB.垂足为E.则AE⊥平面PBC. ∴AE的长等于点D到平面PBC的距离.而.∴.---5分 即点D到平面PBC的距离为.------6分 (Ⅱ) ∵PA⊥底面ABCD.∴平面PAD⊥底面ABCD. 引CM⊥AD于M.MN⊥PD于N.则CM⊥平面PAD. ∴MN是CN在平面PAD上的射影. 由三垂线定理可知CN⊥PD. ∴∠CNM是二面角的平面角.----9分 依题意.. ∴.∴. 可知.∴. .∴二面角的大小为-- 12分 解法二:如图, A为原点.分别以AD.AB.AP为x轴.y轴.z轴建立空间直角坐标系. (Ⅰ)依题意.. ∴. ∴. 则... . ∴... 设平面PBC的一个法向量为.则 令.得. 则点D到平面PBC的距离等于.-----6分 (Ⅱ) ∵AB⊥PA.AB⊥AD.∴AB⊥底面PDA.∴平面PDA的一个法向量为. 设平面PDC的一个法向量为. ∵..∴ 令.得.∴. ∵二面角是锐二面角.∴二面角的大小为.--12分
网址:http://m.1010jiajiao.com/timu3_id_513265[举报]
 中,底面
中,底面 为矩形,侧面
为矩形,侧面 底面
底面 ,
, ,
, .
.
 ;
; 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角 的大小.
的大小.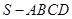 中,底面
中,底面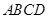 为正方形,侧棱
为正方形,侧棱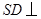 底面
底面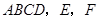 分别为
分别为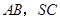 的中点.
的中点.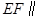 平面
平面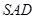 ;
;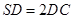 ,求二面角
,求二面角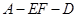 的大小.
的大小.
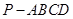 中,底面
中,底面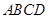 为菱形,
为菱形,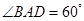 ,
,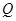 为
为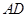 的中点。
的中点。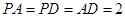
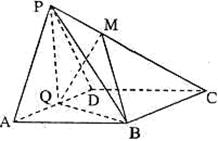
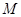 在线段
在线段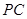 上,
上,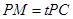 ,试确定
,试确定 的值,使
的值,使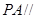 平面
平面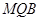 ;
;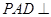 平面ABCD,求二面角
平面ABCD,求二面角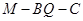 的大小。
的大小。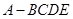 中,底面
中,底面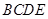 为矩形,侧面
为矩形,侧面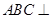 底面
底面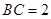 ,
,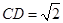 ,
,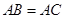 .
.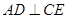 ;
; 与平面
与平面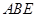 所成的角为
所成的角为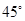 ,求二面角
,求二面角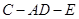 的大小.
的大小.
