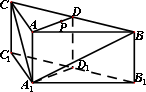
摘要:正棱柱ABC-A1B1C1中.已知A1B⊥AC1.求证: (1)A1B⊥B1C, (2)B1C⊥AC1.
网址:http://m.1010jiajiao.com/timu3_id_512931[举报]
如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD的中点.
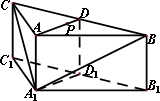
(Ⅰ)在平面ABC内,试作出过点P与平面A1BC平行的直线l,说明理由,并证明直线l⊥平面ADD1A1;
(Ⅱ)设(Ⅰ)中的直线l交AB于点M,交AC于点N,求二面角A-A1M-N的余弦值.
如图,在直三棱柱ABC-A1B1C中,E、F分别是A1B、A1C的中点,点D在B1C上,A1D⊥B1C.
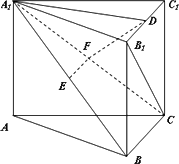
求证:(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
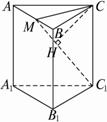
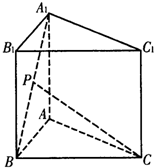 已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B上的点,且PC⊥AB
已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B上的点,且PC⊥AB