摘要：直线过定点P(2.1)且与.轴的正半轴相交于A.B． (1)求使△OAB面积最小时直线的方程． (2)求AB长最小时的直线方程．
网址：http://m.1010jiajiao.com/timu3_id_512888[举报]
已知动圆M过定点P（0，m）(m>0)，且与定直线
相切，动圆圆心M的轨迹方程为C，直线
过点P 交曲线C于A、B两点。
(1)若交
轴于点S,求
的取值范围；
（2）若的倾斜角为
，在
上是否存在点E使△ABE为正三角形? 若能，求点E的坐标；若不能，说明理由.
已知动圆M过定点P（0，m）(m>0)，且与定直线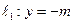
相切，动圆圆心M的轨迹方程为C，直线
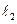过点P 交曲线C于A、B两点。
(1)若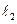交
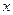轴于点S,求
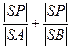的取值范围；
（2）若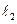的倾斜角为
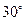，在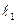
上是否存在点E使△ABE为正三角形? 若能，求点E的坐标；若不能，说明理由.
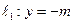相切，动圆圆心M的轨迹方程为C，直线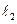过点P 交曲线C于A、B两点。(1)若
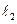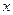交轴于点S,求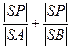的取值范围；（2）若
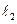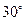的倾斜角为，在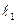上是否存在点E使△ABE为正三角形? 若能，求点E的坐标；若不能，说明理由.
如图在直角坐标系xoy中，圆O与x轴交于A、B两点，且|AB|=4，定直线l垂直于x轴正半轴，且到圆心O的距离为4，点P是圆O上异于A、B的任意一点，直线PA、PB分别交l于点M、N．（1）若∠PAB=30°，求以MN为直径的圆的方程；
（2）当点P变化时，求证：以MN为直径的圆必过圆O内一定点．
，0），F2（
，0），且椭圆短轴的两个端点与F2构成正三角形。
恒为定值，求m的值。