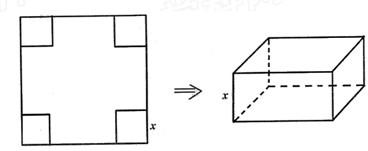
摘要：从边长为2a的正方形铁片四个角各截去一个边长为x的正方形.然后折成一个无盖的长方体的盒子.要求长方体的高度x与底面正方形的边长的比不超过正常数m. (1)把铁盒的体积V表示为x的函数.并指出其定义域, (2)x为何值时.容量V有最大值.
网址：http://m.1010jiajiao.com/timu3_id_512700[举报]
从边长为2a的正方形铁片的四个角各截去一个边为x的正方形，再将四边向上折起，做成一个无盖的长方形铁盒，要求长方体的高度与底面边的比值不超过常数t（t＞0）．试问当x取何值时，容量V有最大值．
查看习题详情和答案>>
查看习题详情和答案>>
从边长为2a的正方形铁片的四个角各截去一个边长为x的正方形，再将四边向上折起，做成一个无盖长方体铁盒，要求长方体的高度与底面边长的比值不超过常数t（t＞0）.试问当x取何值时，容积V有最大值.
查看习题详情和答案>>
从边长为2a的正方形铁片的四个角各截去一个边长为x的正方形，再将四边向上折起，做成一个无盖长方体铁盒，要求长方体的高度与底面边长的比值不超过常数t（t＞0）.试问当x取何值时，容积V有最大值.
查看习题详情和答案>>
