摘要：设点O是直角坐标系的原点.点M在直线:上移动.动点N在线段MO的延长线上.且满足·． (1)求动点N的轨迹方程, (2)当时.求|MN|的最小值． 高三数学教学案 第八章 圆锥曲线 第十课时 求轨迹方程(二) 考纲摘录 使学生进一步理解轨迹的概念.会使用除直接法和定义法外的其他方法求轨迹及轨迹 方程． 知识概要 相关点法.参数法.交轨法． 基础练习
网址：http://m.1010jiajiao.com/timu3_id_512502[举报]
(设点O是直角坐标系的原点，点M在直线l∶x＝－p(p＞0)上移动，动点在线段MO的延长线上，且满足|MN|＝|MO|·|NO|．
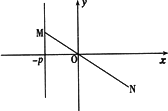
(Ⅰ)求动点N的轨迹方程；
(Ⅱ)当p＝1时，求|MN|的最小值．
在直角坐标系中，已知一个圆心在坐标原点，半径为2的圆，从这个圆上任意一点P向y轴作垂线段
，
为垂足．
(1)求线段中点M的轨迹C的方程；
(2)过点Q(－2，0)作直线l与曲线C交于A、B两点，设N是过点(－
，0)，且以
为方向向量的直线上一动点，满足
(O为坐标原点)，问是否存在这样的直线l，使得四边形OANB为矩形？若存在，求出直线l的方程；若不存在，说明理由．
平面直角坐标系xoy中，直线x-y+1=0截以原点O为圆心的圆所得的弦长为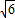
（1）求圆O的方程；
（2）若直线l与圆O切于第一象限，且与坐标轴交于D，E，当DE长最小时，求直线l的方程；
（3）设M，P是圆O上任意两点，点M关于x轴的对称点为N，若直线MP、NP分别交于x轴于点（m，0）和（n，0），问mn是否为定值？若是，请求出该定值；若不是，请说明理由．
查看习题详情和答案>>
（1）求圆O的方程；
（2）若直线l与圆O切于第一象限，且与坐标轴交于D，E，当DE长最小时，求直线l的方程；
（3）设M，P是圆O上任意两点，点M关于x轴的对称点为N，若直线MP、NP分别交于x轴于点（m，0）和（n，0），问mn是否为定值？若是，请求出该定值；若不是，请说明理由．
查看习题详情和答案>>
