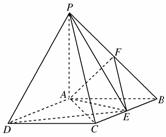
摘要:如图.四棱锥P-ABCD中.底面ABCD是菱形.并且∠DAB=60°.侧面PAD为正三角形.其所在平面垂直于底面ABCD. (1)求证:AD⊥PB, (2)设E为BC边的中点.F为PC中点.求证:平面DEF⊥平面ABCD. 高三数学教学案 第九章 立体几何 第九课时 异面直线所成的角 考纲摘录 掌握空间两条直线所成角的概念. 知识概要
网址:http://m.1010jiajiao.com/timu3_id_512399[举报]
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=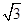 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
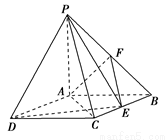
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有 ;
;
(3)当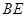 为何值时,
为何值时,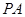 与平面
与平面 所成角的大小为45°.
所成角的大小为45°.
查看习题详情和答案>>
如图,四棱锥P-ABCD中,底面ABCD是正方形,O是正方形ABCD的中心,PO⊥底面ABCD,E是PC的中点,求证:
(1)PA∥平面BDE;
(2)平面PAC⊥平面BDE.

查看习题详情和答案>>
如图,四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=AD=1,AB=2,点E是AB上一点,当二面角P-EC-D的平面角为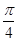 时,AE=( )
时,AE=( )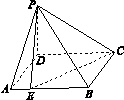
| A.1 | B. | C.2-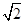 | D.2-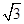 |
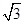 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.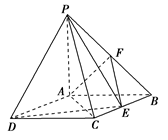
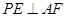 ;
;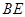 为何值时,
为何值时,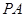 与平面
与平面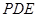 所成角的大小为45°.
所成角的大小为45°.