摘要：如图.在四棱锥P-ABCD中.PA⊥底面ABCD. 底面各边都相等.M是PC上的一动点.当点M满 足 时.平面MBD⊥平面PCD． 例题讲解 例1.如图.ABCD是边长为的菱形.∠A=60°.PC⊥平面ABCD.PC=.E是PA的中点.(1)求证:平面BDE⊥平面ABCD,(2)求E到平面PBC的距离． 例2.ABC-A1B1C1是正三棱柱.底面边长为.D.E分别是BB1.CC1上的点.BD=.EC=．(1)求证:平面ADE⊥平面ACC1A1,(2)求截面△ADE的面积． 例3.如图.ABCD是正方形.E.F分别是AD.BC上的点.EF∥AB.EF交AC于点O.以EF为棱把它折成直二面角A-EF-D后.求证:不论EF怎样移动.∠AOC是定值． 课后作业 班级 学号 姓名
网址：http://m.1010jiajiao.com/timu3_id_512391[举报]
如图，在四棱锥P－ABCD中，PA⊥底面ABCD，底面ABCD为正方形，PA＝AB＝2，M, N分别为PA, BC的中点．
（Ⅰ）证明：MN∥平面PCD；
（Ⅱ）求MN与平面PAC所成角的正切值．
如图，在四棱锥P－ABCD中，PA⊥底面ABCD，底面ABCD为正方形，PA＝AB＝2，M, N分别为PA, BC的中点．
（Ⅰ）证明：MN∥平面PCD；
（Ⅱ）求MN与平面PAC所成角的正切值．
查看习题详情和答案>>
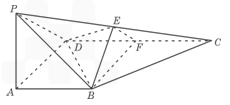
如图，在四棱锥P－ABCD中，PA⊥底面ABCD,
DAB为直角，AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.
（Ⅰ）试证：CD⊥平面BEF;
（Ⅱ）设PA＝k·AB，且二面角E-BD-C的平面角大于30°，求k的取值范围.
DAB为直角，AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.（Ⅰ）试证：CD⊥平面BEF;
（Ⅱ）设PA＝k·AB，且二面角E-BD-C的平面角大于30°，求k的取值范围.
如图，在四棱锥P－ABCD中，PA
底面ABCD,
DAB为直角，AB‖CD,AD=CD=24B,E、F分别为PC、CD的中点.
,且二面角E-BD-C的平面角大于
,求
的取值范围.