摘要：如图在直角梯形ABCD中.∠BAD=∠ADC=90°.CD=DA= a.AB=2a.SA⊥平面ABCD.且SA= a. (1)求证:△SAD.△SAB.△SDC.△SCB都是直角三角形, (2)在SD上取点M.SC交平面ABM于N.求证:四边形ABNM为直角三梯形, (3)若SM=.写出BM=的表达式.并求当为何值时.BM最小?最小值是多少? 高三数学教学案 第九章 直线.平面.简单几何体 第五课时 线面平行与面面平行 基础知识 掌握直线和平面平行.两个平面平行的判定定理和性质定理． 知识概要
网址：http://m.1010jiajiao.com/timu3_id_512274[举报]
如图所示，在直角梯形ABCD中，∠BAD=∠ADC=90°，CD=DA=a，AB=2a，SA⊥平面ABCD，且SA=a．
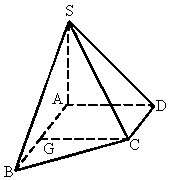
(1)求证：△SAD、△SAB、△SCB、△SDC都是直角三角形；
(2)在SD上取点M，SC交平面ABM于N，求证：四边形ABNM为直角梯形．
查看习题详情和答案>>如图所示，在直角梯形
ABCD中，∠BAD=∠ADC=90°，CD=DA=a，AB=2a，SA⊥平面ABCD，且SA=a．
(1)
求证：△SAD、△SAB、△SCB、△SDC都是直角三角形；(2)
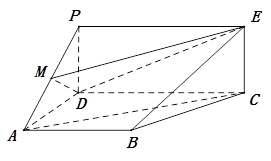
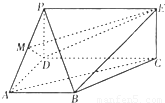
在SD上取点M，SC交平面ABM于N，求证：四边形ABNM为直角梯形． 查看习题详情和答案>>如图，PDCE为矩形，ABCD为梯形，平面PDCE⊥平面ABCD，∠BAD＝∠ADC＝90°，AB＝AD＝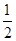
CD＝1，PD＝
。
（I）若M为PA中点，求证：AC∥平面MDE；
（II）求直线PA与平面PBC所成角的正弦值；
（III）在线段PC上是否存在一点Q（除去端点），使得平面QAD与平面PBC所成锐二面角的大小为
？
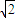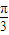CD=1，PD=
．
．
CD＝1，PD＝
.
？