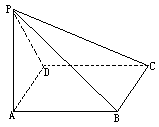
摘要：四棱锥P-ABCD的底面为正方形PD⊥底面ABCD.PD=AD=1.设点C到平面PAB的距离为d1.点B到平面PAC的距离为d2.BC到平面PAD的距离为d3.则有( ) A．d3＜d1＜d2 B．d1＜d2＜d3 C．d1＜d3＜d2 D．d2＜d1＜d3
网址：http://m.1010jiajiao.com/timu3_id_512178[举报]
四棱锥
P－ABCD的底面为正方形，PD⊥平面ABCD，PD=AD=1，设点C到平面PAB的距离为a，点B到平面PAC的距离为b，则有[
]|
A ．1＜a＜b |
B ．a＞b＞1 |
|
C ．a＜1＜b |
D ．b＜a＜1 |
已知：四棱锥P－ABCD的底面为正方形，PA⊥底面ABCD，E、F分别为AB、PD的中点，PA＝a，∠PDA＝45°
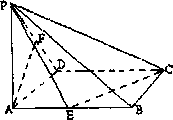
(1)求证：AF∥平面PCE；
(2)求证：平面PAC⊥PBD；
(3)点D到平面PCE的距离．
如图，四棱锥P－ABCD的底面为正方形，侧棱PA⊥底面ABCD，且PA＝AD＝2，E，F，H分别是线段PA，PD，AB的中点．
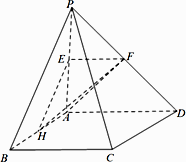
(Ⅰ)求证：PB∥平面EFH；
(Ⅱ)求证：PD⊥平面AHF；
(Ⅲ)求二面角H―EF―A的大小．
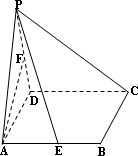
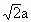，则它的五个面中，互相垂直的面是________．(把互相垂直的面都填上)
