如图，已知平面ABC⊥平面BCDE，△DEF与△ABC分别是棱长为1与2的正三角形，AC∥DF，四边形BCDE为直角梯形，DE∥BC，BC⊥CD，CD＝1，点G为△ABC的重心，N为AB中点，＝λ(λ∈R，λ＞0)．

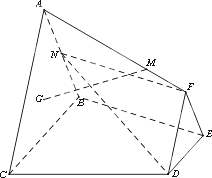
(Ⅰ)当时，求证：GM∥平面DFN．

(Ⅱ)若直线MN与CD所成角为，试求二面角M－BC－D的余弦值．

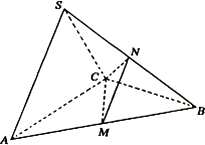
在三棱锥S－ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA＝SC＝2，M、N分别为AB、SB的中点．

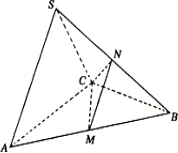
(1)证明：AC⊥SB；

(2)求二面角N－CM－B的大小；

(3)求点B到平面CMN的距离．

在三棱锥S－ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA＝SC＝，M、N分别为AB、SB的中点．

(1)证明：AC⊥SB；

(2)求二面角N－CM－B的余弦值；

(3)求B点到平面CMN的距离．