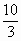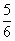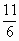摘要：(一) 选择题 1.1∥2.a.b与1.2都垂直.则a.b的关系是 A.平行 B.相交 C.异面 D.平行.相交.异面都有可能 2.异面直线a.b.a⊥b.c与a成300.则c与b成角范围是 A.[600.900] B.[300.900] C.[600.1200] D.[300.1200] 3.正方体AC1中.E.F分别是AB.BB1的中点.则A1E与C1F所成的角的余弦值是 A. B. C. D. 4.在正△ABC中.AD⊥BC于D.沿AD折成二面角B-AD-C后.BC=AB.这时二面角B-AD-C大小为 A.600 B.900 C.450 D.1200 5.一个山坡面与水平面成600的二面角.坡脚的水平线为AB.甲沿山坡自P朝垂直于AB的方向走30m.同时乙沿水平面自Q朝垂直于AB的方向走30m.P.Q都是AB上的点.若PQ=10m.这时甲.乙2个人之间的距离为 A. B. C. D. 6.E.F分别是正方形ABCD的边AB和CD的中点.EF交BD于O.以EF为棱将正方形折成直二面角如图.则∠BOD= A.1350 B.1200 C.1500 D.900 7.三棱锥V-ABC中.VA=BC.VB=AC.VC=AB.侧面与底面ABC所成的二面角分别为α.β.γ.则cosα+cosβ+cosγ等于 A.1 B.2 C. D. 8.正n棱锥侧棱与底面所成的角为α.侧面与底面所成的角为β.tanα∶tanβ等于 A. B. C. D. 9.一个简单多面体的各面都是三角形.且有6个顶点.则这个简单多面体的面数是 A.4 B.6 C.8 D.10 10.三棱锥P-ABC中.3条侧棱两两垂直.PA=a.PB=b.PC=c.△ABC的面积为S.则P到平面ABC的距离为 A. B. C. D. 11.三棱柱ABC-A1B1C1的体积为V.P.Q分别为AA1.CC1上的点.且满足AP=C1Q.则四棱锥B-APQC的体积是 A. B. C. D. 12.多面体ABCDEF中.已知面ABCD是边长为3的正方形.EF∥AB.EF=.EF与面AC的距离为2.则该多面体的体积为 A. B.5 C.6 D.
网址：http://m.1010jiajiao.com/timu3_id_510411[举报]
选择题．
(1)
为了得到函数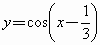
的图像，只需将余弦函数图像上各点
[
]A
．向左平移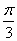
个单位长度
B
．向右平移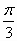
个单位长度
C
．向左平移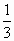
个单位长度
D
．向右平移
个单位长度
(2)
为了得到函数
的图像，只需将函数
的图像上各点( )即可．
[
]A
．横坐标伸长为原来的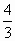
倍，纵坐标不变
B
．横坐标缩短为原来的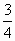
倍，纵坐标不变
C
．纵坐标伸长为原来的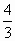倍，横坐标不变
D
．纵坐标缩短为原来的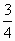
倍，横坐标不变
(3)
将函数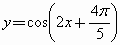
的图像上各点向右平行移动
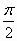个单位长度，再把横坐标缩短为原来的一半，纵坐标伸长为原来的4倍，则所得到的图像的函数解析式是
[
]|
A ． |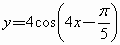
B ． |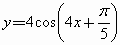
|
C ． |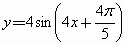
D ． |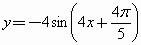
选择题．
(1)
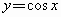
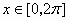的图像与直线
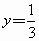的交点的个数为
[
]|
A ．0 |
B ．1 |
C ．2 |
D ．3 |
(2)
当x∈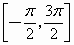
时，函数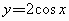
[ ]
A
．在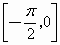
，
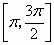上是增加的，在
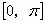上是减少的
B
．在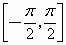
上是增加的，在
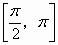上是减少的
C
．在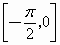
，
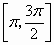上是减少的，在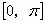上是增加的
D
．在∪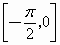
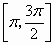上是增加的，在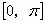上是减少的
(3)
下列命题中正确的是[
]A
．函数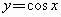
在
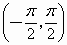上是减少的
B
．函数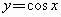在
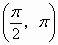上是减少的
C
．函数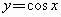在
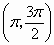上是减少的
D
．函数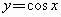在
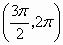上是减少的
(4)
函数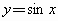
和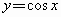
都是增加的区间是
[
]A
．
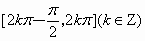
B
．
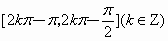
C
．
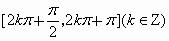
D
．
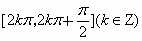查看习题详情和答案>>
选择题．
(1)
下列几何体中是棱柱的有[
]
|
(A)1 个 |
(B)2 个 |
(C)3 个 |
(D)4 个 |
(2)
下列命题正确的是[
](A)
有两个面平行，其余各面都是四边形的几何体叫棱柱．(B)
有两个面平行，其余各面都是平行四边形的几何体叫棱柱．(C)
有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱．(D)
用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台．(3)
如下图，右边长方体中由左边的平面图形围成的是[
]
(4)
充满气的车轮内胎可由下面某个图形绕对称轴旋转而成，这个图形是[
]
选择题．
(1)
由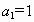
，
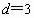确定的等差数列
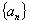，当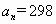
时，序号n等于
[
］|
(A)99 ． |
(B)100 ． |
(C)96 ． |
(D)101 ． |
(2)
一个蜂巢里有1只蜜蜂．第1天，它飞出去找回了5个伙伴；第2天，6只蜜蜂飞出去，各自找回了5个伙伴……如果这个找伙伴的过程继续下去，第6天所有的蜜蜂都归巢后，蜂巢中一共有( )只蜜蜂．[
]|
(A)55986 ． |
(B)46656 ． |
(C)216 ． |
(D)36 ． |
(3)
预测人口的变化趋势有多种方法，“直接推算法”使用的公式是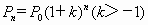
，其中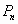
为预测期人口数，
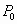为初期人口数，k为预测期内年增长率，n为预测期间隔年数．如果在某一时期有－1＜k＜0，那么在这期间人口数
[
]|
(A) 呈上升趋势． |
(B) 呈下降趋势． |
(C) 摆动变化． |
(D) 不变． |
(4)
《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一．书中有一道这样的题目：把100个面包分给5个人，使每人所得成等差数列，且使较大的三份之和的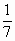
是较小的两份之和，问最小1份为
[
]|
(A) |
(B) |
(C) |
(D) |
选择题：
(1)
已知
，
，
，则
[
]|
(A)A 、B、D三点共线 |
(B)A 、B、C三点共线 |
|
(C)B 、C、D三点共线 |
(D)A 、C、D三点共线 |
(2)
已知正方形ABCD的边长为1，
，
，
，则
等于
[
]|
(A)0 |
(B)3 |
(C) |
(D) |
(3)
已知
，
，
，
，且四边形ABCD为平行四边形，则
[
]|
(A)a ＋b＋c＋d＝0 |
(B)a －b＋c－d＝0 |
|
(C)a ＋b－c－d＝0 |
(D)a －b－c＋d＝0 |
(4)
已知D、E、F分别是△ABC的边BC、CA、AB的中点，且
，
，
，则①
；②
；③
；④
中正确的等式的个数为
[
]|
(A)1 |
(B)2 |
(C)3 |
(D)4 |
(5)
若
，
是夹角为60°的两个单位向量，则
；
的夹角为
[
]|
(A)30° |
(B)60° |
(C)120° |
(D)150° |
(6)
若向量a、b、c两两所成的角相等，且
，
，
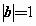，则
等于
[
]|
(A)2 |
(B)5 |
(C)2 或5 |
(D)  |
(7)
等边三角形ABC的边长为1，
，
，
，那么a·b＋b·c＋c·a等于
[
]|
(A)3 |
(B) －3 |
(C) |
(D) |
