摘要:综合试题的热点问题: 热点之一:圆锥曲线的定义.圆锥曲线方程 圆锥曲线定义是其一切几何性质的“根 与“源 .是建立曲线方程的基础.揭示了圆锥曲线上的点与焦点及准线间的关系.是解几综合题的重要背景.圆锥曲线的方程是研究几何性质的重要载体. 热点之二:函数与方程的思想 函数与方程的思想是贯穿于解析几何的一条主线.很多解几综合题往往都是以最值问题或圆锥曲线的基本量的求解为依托.通过转化.运用函数与方程的思想加以解决. 热点之三:与圆锥曲线有关的轨迹问题 解析几何的核心就是用方程的思想研究曲线.用曲线的性质研究方程.轨迹问题正是体现这一思想的重要形式.运用定义法.代入法.参数法.结合问题的几何特征.可以较好的求解. 热点之四:曲线组合 除了直线和圆锥曲线是传统的结合外.04年的高考题大量出现了圆与双曲线.圆与抛物线.双曲线与抛物线等的结合. 热点之五:与平面向量.导数等新增内容相结合 利用一切可以利用的机会有机结合. 热点之六:最值及离心率范围问题 通过求最值及离心率的范围问题达到与函数.方程.不等式等主干知识链接.
网址:http://m.1010jiajiao.com/timu3_id_510103[举报]
抛物线的顶点在原点,它的准线过双曲线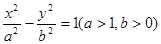 的一个焦点,并于双曲线的实轴垂直,已知抛物线与双曲线的交点为
的一个焦点,并于双曲线的实轴垂直,已知抛物线与双曲线的交点为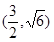 ,求抛物线的方程和双曲线的方程。
,求抛物线的方程和双曲线的方程。
【解析】本试题主要考查了抛物线方程的求解以及双曲线与抛物线的交点问题的综合运用。
查看习题详情和答案>>
设命题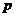 :方程
:方程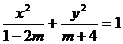 表示的图象是双曲线;命题
表示的图象是双曲线;命题 :
: ,
,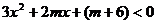 .求使“
.求使“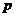 且
且 ”为真命题时,实数
”为真命题时,实数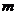 的取值范围.
的取值范围.
【解析】本试题考查了双曲线的方程的运用,以及不等式有解时,参数的取值范围问题,以及符合命题的真值的判定综合试题。
查看习题详情和答案>>
抛物线的顶点在原点,它的准线过双曲线 的一个焦点,并于双曲线的实轴垂直,已知抛物线与双曲线的交点为
的一个焦点,并于双曲线的实轴垂直,已知抛物线与双曲线的交点为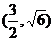 ,求抛物线的方程和双曲线的方程。
,求抛物线的方程和双曲线的方程。
【解析】本试题主要考查了抛物线方程的求解以及双曲线与抛物线的交点问题的综合运用。
查看习题详情和答案>>
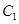 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线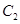 :
: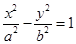 的一个焦点
的一个焦点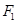 且垂直于
且垂直于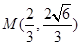 .
.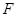 的坐标;
(Ⅱ)求双曲线
的坐标;
(Ⅱ)求双曲线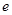 .
.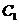 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线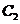 :
: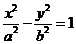 的一个焦点
的一个焦点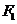 且垂直于
且垂直于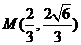 .
.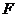 的坐标;
(Ⅱ)求双曲线
的坐标;
(Ⅱ)求双曲线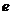 .
.