摘要:22.对于函数f(x).若存在x0∈R.使f(x0)=x0成立.则称x0为f(x)的不动点.如果函数有且只有两个不动点0.2.且 ⑴求函数f(x)的解析式, ⑵已知各项不为零的数列.求数列通项, ⑶如果数列满足.求证:当时.恒有成立.
网址:http://m.1010jiajiao.com/timu3_id_509974[举报]
(本小题满分14分)已知定义在实数集上的函数fn(x)=xn,n∈N*,其导函数记为 ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
(1)试求a的值;
(2)记函数
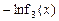 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值;
(3)对于(2)中的b,设函数 ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.
(本小题满分14分)已知定义在实数集上的函数fn(x)=xn,n∈N*,其导函数记为 ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
(1)试求a的值;
(2)记函数
 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值;
(3)对于(2)中的b,设函数 ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.
查看习题详情和答案>>
(本小题满分14分)
已知定义域为[0, 1]的函数f(x)同时满足:
①对于任意的x [0, 1],总有f(x)≥0;
[0, 1],总有f(x)≥0;
②f(1)=1;
③若0≤x1≤1, 0≤x2≤1, x1+x2≤1, 则有f (x1+x2) ≥ f (x1)+f (x2).
(1)试求f(0)的值;
(2)试求函数f(x)的最大值;
(3)试证明:当x , n
, n N+时,f(x)<2x.
N+时,f(x)<2x.
查看习题详情和答案>>
 [0, 1],总有f(x)≥0;
[0, 1],总有f(x)≥0;  , n
, n
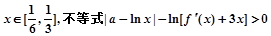 成立,求实数a的取值范围;
成立,求实数a的取值范围; 在[0,2]上恰有两个不同的实根,求实数b的取值范围.
在[0,2]上恰有两个不同的实根,求实数b的取值范围.