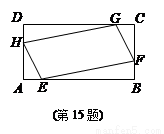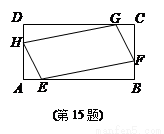摘要：21．⑴证:∵AE＝BF＝x.∴A′(a,0,a).C′(0,a,a).E(a,x,0).F(a-x,a,0). --4分 ∴A′F⊥C′E. ⑵由BF＝x.EB＝a-x. 则当且仅当 时等号成立.此时E.F分别为AB.BC的中点. 取EF的中点M.连BM.则BM⊥EF.根据三垂线定理知EF⊥B1M. ∴∠B1MB即为二面角B1-EF-B的平面角. 在Rt△BMF中. 在Rt△B1BM中. ∴二面角B1-EF-B的大小是.
网址：http://m.1010jiajiao.com/timu3_id_509132[举报]
某地政府为科技兴市，欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分)，形状为直角梯形QPRE(线段EQ和RP为两个底边)，已知AB＝2 km，BC＝6 km，AE＝BF＝4 km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分．分别以直线AB，AD为x轴和y轴建立平面直角坐标系．
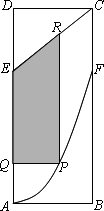
(1)求曲线段AF所在抛物线的方程；
(2)设点P的横坐标为x，高科技工业园区的面积为S．试求S关于x的函数表达式，并求出工业园区面积S的最大值．
如图，正方体
，棱长为a，E、F分别为AB、BC上的点，且AE＝BF＝x．
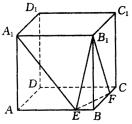
（1）当x为何值时，三棱锥
的体积最大？
（2）求三棱椎
的体积最大时，二面角
的正切值；
（3）（理科做）求异面直线
与
所成的角的取值范围．
查看习题详情和答案>>
