摘要:22. 设x1.x2是函数的两个极值点.且. (1) 用a表示.并求出a的取值范围. (2) 证明: . (3) 若函数 ,证明:当且x1<0时, .
网址:http://m.1010jiajiao.com/timu3_id_508508[举报]
(本小题满分14分)已知函数
(1)求函数 的单调递增区间;
的单调递增区间;
(2)记函数 的图象为曲线C.设点A(x1,y1),B(x2,y2)是曲线C上的不同两点.如果在曲线C上存在点M(x0,y0),使得:①
的图象为曲线C.设点A(x1,y1),B(x2,y2)是曲线C上的不同两点.如果在曲线C上存在点M(x0,y0),使得:① ;②曲线C在点M处的切线平行于直线AB,则称函数F(x)夺在“中值相依切线”,
;②曲线C在点M处的切线平行于直线AB,则称函数F(x)夺在“中值相依切线”,
试问:函数f(x)是否存在“中值相依切线”,请说明理由.
查看习题详情和答案>>
(本小题满分14分)已知f(x)=![]() (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)=![]() 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
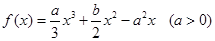 的两个极值点,且
的两个极值点,且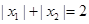 。
。 ,并求出a的取值范围.
,并求出a的取值范围.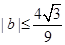 .
.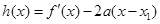 ,证明:当
,证明:当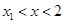 且x1<0时,
且x1<0时, 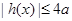 .
. ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
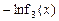 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值; ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明. ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值; ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.