摘要:6.讲解例3.例4 例3 实数x分别取什么值时.复数 z二x2+x一6+(x2-2x一15)i 是纯虚数?(4)零? 分析:因为xR.所以x2+x一6.x2-2x-15都是实数.由复数:’.+航是实数虚数.纯虚数与零的条件可以确定实数x的值. 解:(1)当x2-2x一15二0.即x二一3或x二5时 (2)当x2-2x-150.即x-3且x5 (3)当x2+x一6=0且x2-2x一150.即x=2 (4)当x2+x一6=0且x2-2x一15=0.即x=-3 例4 求适合下列方程中的z与y(x.yR)的值. (1)x2十2+I=y2+9十(y-2)i (2)2x2-5x十3+(y2+y一6)I=0. 分析:因为x.y.所以由两个复数相等的定义个方程组.可求出z.9的值 解:(1)根据复数相等的定义 x2十2二y2十9. x-3=y-2. 所以. x=4.y=3. 得方程组 (2)根据复数相等的定义.得方程组 2x2-5x十3=0. y2十y-6=0. X=,或x=1 Y=-3,或y=2
网址:http://m.1010jiajiao.com/timu3_id_508032[举报]
给出下列五个结论其中正确的是( )
①若实数x,y满足(x-2)2+y2=3,则
的最大值为
;②椭圆
+
=1与椭圆
+
=1有相同的离心率;③双曲线
+
=1的焦点坐标是(1,0),(-1,0)④圆x2+y2=1与直线y=kx+2没有 公共点的充要条件是k∈(-
,
)⑤设a>1,则双曲线
-
=1的离心率e的取值范围是(
,
).
①若实数x,y满足(x-2)2+y2=3,则
| y |
| x |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 2 |
| 2y2 |
| 3 |
| x2 |
| 2-k |
| y2 |
| 3-k |
| 3 |
| 3 |
| x2 |
| a2 |
| y2 |
| (a+1)2 |
| 2 |
| 5 |
查看习题详情和答案>>
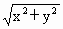 的最小值为_________.
的最小值为_________. 的最小值为_________.
的最小值为_________.