摘要:20.函数对任意的实数m.n有且当时有 . (1)求证在R上为增函数, (2)若解不等式.
网址:http://m.1010jiajiao.com/timu3_id_508009[举报]
函数y=f(x)定义在R上,对于任意实数m,n,恒有f(m+n)=f(m)•f(n),且当x>0时,0<f(x)<1.
Ⅰ.求证:f(0)=1;
Ⅱ.当x<0时,比较f(x)与1的大小;
Ⅲ.判断f(x)在R上的单调性,并证明你的结论;
Ⅳ.如果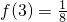 ,试求f(2002)的值.
,试求f(2002)的值.
查看习题详情和答案>>
设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)•f(n),且当x>0 时,0<f(x)<1.
(Ⅰ)若f(1)=
,求
的值;
(Ⅱ)求证:f(0)=1,且当x<0时,有f(x)>1;
(Ⅲ)判断f(x)在R上的单调性,并加以证明.
查看习题详情和答案>>
(Ⅰ)若f(1)=
| 1 |
| 2 |
| f(1)+f(2) |
| f(1) |
(Ⅱ)求证:f(0)=1,且当x<0时,有f(x)>1;
(Ⅲ)判断f(x)在R上的单调性,并加以证明.
设函数y=f(x)的定义域为(0,+∞),且对任意的正实数x,y,均有f(xy)=f(x)+f(y)恒成立.已知f(2)=1,且当x>1时,f(x)>0.
(1)求f(
)的值,试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
(2)一个各项均为正数的数列{an},它的前n项和是Sn,若a1=3,且f(Sn)=f(an)+f(an+1)-1(n≥2,n∈N*),求数列{an}的通项公式;
(3)在(2)的条件下,是否存在实数M,使2n•a1•a2…an≥M•
•(2a1-1)•(2a2-1)…(2an-1)对于一切正整数n均成立?若存在,求出M的范围;若不存在,请说明理由.
查看习题详情和答案>>
(1)求f(
| 1 |
| 2 |
(2)一个各项均为正数的数列{an},它的前n项和是Sn,若a1=3,且f(Sn)=f(an)+f(an+1)-1(n≥2,n∈N*),求数列{an}的通项公式;
(3)在(2)的条件下,是否存在实数M,使2n•a1•a2…an≥M•
| 2n+3 |