摘要：解.B得直线AB即直线MN方程为y=x+3.代入椭圆C1的方程并整理.得(a2+b2)x2+6a2x+9a2-a2b2＝0 (*) 设M(x1,y1).N(x2,y2).则 x1+x2＝- ∵A是弦MN的中点.∴x1+x2=-4.故由得a2=2b2, 又b2=a2-c2.∴a=.从而椭圆离心率e1=. ∵A为C2的焦点.且相应准线l方程为.即.过B作BB0⊥l于B0.则由双曲线定义知.e2=. 法二:设M(x1.y1),N(x2,y2),则x1+x2＝4.y1+y2＝2,且 .
网址：http://m.1010jiajiao.com/timu3_id_507870[举报]
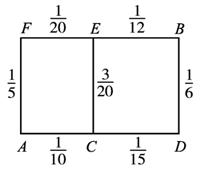
现在小型轿车慢慢进入百姓家庭，但是另一个问题相继暴露出来--堵车．李先生居住在城市的A处，准备开车到B处上班，若该地各路段发生堵车事件是相互独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如图所示（例如A→C→D并作两个路段：路段AC发生堵车事件的概率是| 1 |
| 10 |
| 1 |
| 15 |
（1）请你为李先生选择一条由A到B的路线，使得沿途经过的路口尽可能少，且发生堵车的概率最小；
（2）若该路线A→C→F→B中遇到堵车的次数为随机变量X，求X的数学期望．
某先生居住在城镇的A处，准备开车到单位B处上班，若该地各路段发生堵车事件都是独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率，如图．（ 例如：A→C→D算作两个路段：路段AC发生堵车事件的概率为| 1 |
| 10 |
| 1 |
| 15 |
（1）请你为其选择一条由A到B的路线，使得途中发生堵车事件的概率最小；
（2）若记ξ路线A→（3）C→（4）F→（5）B中遇到堵车次数为随机变量ξ，求ξ的数学期望Eξ．
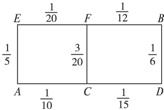某先生居住在城镇的A处，准备开车到单位B处上班，若该地各路段发生堵车事件都是独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如如图所示．（例如：A→C→D算作两个路段：路段AC发生堵车事件的概率为| 1 |
| 10 |
| 1 |
| 15 |
（1）请你为其选择一条由A到B的路线，使得途中发生堵车事件的概率最小；
（2）若记路线A→C→F→B中遇到堵车次数为随机变量X，求X的概率分布． 查看习题详情和答案>>
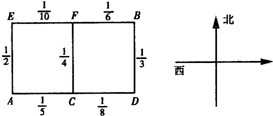某人居住在城镇的A处，准备开车到单位B处上班，若该地各路段发生堵车事件都是相互独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如图．（例如：A→C→D算作两个路段：路段AC发生堵车事件的概率为
，路段CD发生堵车事件的概率为
）.