摘要:(17) 由.得. ∵DABC是锐角三角形. . ----------..3分 设DABC外接圆半径为R.由正弦定理得 ---..9分 若B=C.则 若B¹C.则 ---------..12分 ∵PA^底面ABCD AD是PD在平面ABCD内的射影. ∵CDÌ平面ABCD.且CD^AD. 故CD^PD .------...-4分 (Ⅱ)取CD中点G.连结EG.FG ∵E.F分别是AB.PC的中点.\EG//AD.FG//PD. \平面EFG//平面PAD.\EF//平面PAD. -----..--8分 (Ⅲ)当平面PCD与平面ABCD成45°角时.直线EF^平面PCD. 证明:G为CD中点.则EG^CD.由(1)知FG^CD. 故ÐEGF为平面PCD 与平面ABCD所成二面角的平面角.即ÐEGF=45°. 从而得ÐADP=45°. AD=AP. 由RtDPAE@RtDCBE.得PE=CE. 又F是PC的中点.\EF^PC. 由CD^EG.CD^FG.得CD^平面EFG.CD^EF.即EF^CD. 故EF^平面PCD. ----..------.----.12分 .----------..4分 (Ⅱ) ∵ 则是首项为.公差为的等差数列. 故.由.可求得.-8分 (Ⅲ) . 则.----.12分 到第年该公司共有名职工,基础工资总额为万元, 房屋补贴总额为: -..2分 万元, ---.--------..4分 医疗费总额为 ----6分 (II) ∴每年房屋补贴和医疗费用的总和不会超过基础工资总额20%. -..-.12分 以为轴.且点在轴的正半轴上建立直角坐标系.则的方程为. 点的坐标为.设点是曲线段上任意一点.则 ..---..4分 (2)设点.点是曲线段上任意一点.依题意: .--.6分 若即.则当时.,---..8分 若即.则当时.,---.10分 若即.则当时..---..12分 . ---.--2分 设 . 故. ------.---..6分 又. 从而 又. .等号在t=4, x=0时取得.-.---.8分 (Ⅱ) 时. . 若恒成立.只要恒成立, 即 -------11分 令 则 故 当u=1时.. 即所求t的范围是.----------..----.14分
网址:http://m.1010jiajiao.com/timu3_id_505517[举报]
解:(Ⅰ)设![]() :
:![]()
![]() ,其半焦距为
,其半焦距为![]()
![]() .则
.则![]() :
:![]() .
.
由条件知![]() ,得
,得![]() .
.
![]() 的右准线方程为
的右准线方程为![]() ,即
,即![]() .
.
![]() 的准线方程为
的准线方程为![]() .
.
由条件知![]() , 所以
, 所以![]() ,故
,故![]() ,
,![]() .
.
从而![]() :
:![]() ,
, ![]() :
:![]() .
.
(Ⅱ)由题设知![]() :
:![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() .
.
由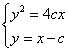 ,得
,得![]() ,所以
,所以![]() .
.
而![]() ,由条件
,由条件![]() ,得
,得![]() .
.
由(Ⅰ)得![]() ,
,![]() .从而,
.从而,![]() :
:![]() ,即
,即![]() .
.
由 ,得
,得![]() .所以
.所以![]() ,
,![]() .
.
故![]() .
.
阅读下面材料:根据两角和与差的正弦公式,有
sin(α+β)=sinαcosβ+coαsinβ ①
sin(α-β)=sinαcosβ-cosαsinβ ②
由①+②得
sin(α+β)+sin(α-β)=2sinαcosβ ③
令α+β=A,α-β=B有α=![]() ,β=
,β=![]()
代入③得sinA+sinB=2sin![]() cos
cos![]() .
.
(Ⅰ)上面的式子叫和差化积公式,类比上述推理方法,根据两角和与差的余弦公式,把cosA-cosB也化成积的形式,要求有推导过程;
(Ⅱ)若△ABC的三个内角A,B,C满足cos2A-cos2B=1-cos2C,试判断△ABC的形状.(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
(2012•泰安一模)下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程
=
x+
必过(
,
);
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握确认这两个变量间有关系;
其中错误的个数是( )
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程
| ? |
| y |
③线性回归方程
| ? |
| y |
| ? |
| b |
| ? |
| a |
. |
| x |
. |
| y |
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握确认这两个变量间有关系;
其中错误的个数是( )
查看习题详情和答案>>
下列四个命题中
①设有一个回归方程y=2-3x,变量x增加一个单位时,y平均增加3个单位;
②命题P:“?x0∈R,x02-x0-1>0“的否定¬P:“?x∈R,x2-x-1≤0”;
③设随机变量X服从正态分布N(0,1),若P(X>1)=p,则P(-l<X<0)=
-p;
④在一个2×2列联表中,由计算得K2=6.679,则有99%的把握确认这两个变量间有关系.
其中正确的命题的个数有( )
附:本题可以参考独立性检验临界值表
①设有一个回归方程y=2-3x,变量x增加一个单位时,y平均增加3个单位;
②命题P:“?x0∈R,x02-x0-1>0“的否定¬P:“?x∈R,x2-x-1≤0”;
③设随机变量X服从正态分布N(0,1),若P(X>1)=p,则P(-l<X<0)=
| 1 |
| 2 |
④在一个2×2列联表中,由计算得K2=6.679,则有99%的把握确认这两个变量间有关系.
其中正确的命题的个数有( )
附:本题可以参考独立性检验临界值表
| P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10. 828 |
| A、1个 | B、2个 | C、3个 | D、4个 |