摘要:21.(1)设动点N的坐标为(x,y).则 -------2分 .因此.动点的轨迹方程为 --4分 (2)设l与抛物线交于点A(x1,y1),B(x2,y2).当l与x轴垂直时. 则由. 不合题意. 故与l与x轴不垂直.可设直线l的方程为y=kx+b,则由-6分 由点A.B在抛物线 又y2=4x, y=kx+b得ky2-4y+4b=0,--------8分 所以--10分 因为解得直线l的斜率的取值范围是.------------------------12分
网址:http://m.1010jiajiao.com/timu3_id_503787[举报]
设
=(a1,a2),
=(b1,b2)定义向量
?
=(a1b1,a2b2),已知
=(2,
),
=(
,0),且点P(x,y)在函数y=sinx的图象上运动,Q在函数y=f(x)的图象上运动,且点P和点Q满足:
=
?
+
(其中O为坐标原点),则函数y=f(x)的最大值A及最小正周期T分别为( )
| a |
| b |
| a |
| b |
|
| 1 |
| 2 |
| n |
| π |
| 3 |
| OQ |
| m |
| OP |
| n |
| A、2,π | ||
| B、2,4π | ||
C、
| ||
D、
|
设a=(a1,a2),b=(b1,b2),定义一种向量积:a?b=(a1,b1)?(b1,b2)=(a1b1,a2b2).已知m=(2,
),n=(
,0),点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动,且满足(x,f(x))=m?n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别( )
| 1 |
| 2 |
| π |
| 3 |
| A、2,π | ||
| B、2,4π | ||
C、
| ||
D、
|
设a=(a1,a2),b=(b1,b2),定义一种向量积:a?b=(a1,b1)?(b1,b2)=(a1b1,a2b2).已知m=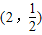 ,n=
,n=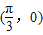 ,点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动,且满足(x,f(x))=m?n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别( )
,点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动,且满足(x,f(x))=m?n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别( )
A.2,π
B.2,4π
C. ,4π
,4π
D. ,π
,π
查看习题详情和答案>>
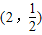 ,n=
,n=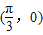 ,点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动,且满足(x,f(x))=m?n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别( )
,点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动,且满足(x,f(x))=m?n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别( )A.2,π
B.2,4π
C.
 ,4π
,4πD.
 ,π
,π查看习题详情和答案>>
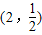 ,n=
,n=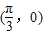 ,点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动,且满足(x,f(x))=m?n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别( )
,点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动,且满足(x,f(x))=m?n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别( ) ,4π
,4π ,π
,π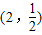 ,n=
,n=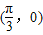 ,点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动,且满足(x,f(x))=m?n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别( )
,点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动,且满足(x,f(x))=m?n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别( ) ,4π
,4π ,π
,π