摘要:(2005湖北卷理第21题.文第22题) 设A.B是椭圆上的两点.点N(1.3)是线段AB的中点.线段AB的垂直平分线与椭圆相交于C.D两点. (Ⅰ)确定的取值范围.并求直线AB的方程, (Ⅱ)试判断是否存在这样的.使得A.B.C.D四点在同一个圆上?并说明理由.
网址:http://m.1010jiajiao.com/timu3_id_503554[举报]
设A、B是椭圆 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定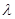 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)当 时求由A、B、C、D四点组成的四边形的面积。
时求由A、B、C、D四点组成的四边形的面积。
查看习题详情和答案>>
(05年湖北卷)(12分)
设A、B是椭圆![]() 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定![]() 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的![]() ,使得A、B、C、D四点在同一个圆上?并说明理由.
,使得A、B、C、D四点在同一个圆上?并说明理由.
(此题不要求在答题卡上画图)
查看习题详情和答案>>
22.
设A、B是椭圆![]() 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定![]() 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的![]() ,使得A、B、C、D四点在同一个圆上?并说明理由.
,使得A、B、C、D四点在同一个圆上?并说明理由.
 相交于A、B两点.
相交于A、B两点. 上的任意两点,M是线段AB的中点,若直线AB、OM的斜率都存在,并记为kAB,kOM,则kAB?kOM为定值.试对双曲线
上的任意两点,M是线段AB的中点,若直线AB、OM的斜率都存在,并记为kAB,kOM,则kAB?kOM为定值.试对双曲线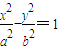 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.