摘要:74.在利用圆锥曲线统一定义解题时.你是否注意到定义中的定比的分子分母的顺序?
网址:http://m.1010jiajiao.com/timu3_id_503199[举报]
在圆锥曲线的学习中,我们已经学习了它的标准方程,以椭圆![]() =1(a>b>0)为例说明此方程就是以F1(-c,0),F2(c,0)为焦点,长轴长为2a的椭圆的方程.怎样利用曲线与方程的定义说明上述问题?
=1(a>b>0)为例说明此方程就是以F1(-c,0),F2(c,0)为焦点,长轴长为2a的椭圆的方程.怎样利用曲线与方程的定义说明上述问题?
(2010•福建模拟)已知中心的坐标原点,以坐标轴为对称轴的双曲线C过点Q(2,
),且点Q在x轴上的射影恰为该双曲线的一个焦点F1
(Ⅰ)求双曲线C的方程;
(Ⅱ)命题:“过椭圆
+
=1的一个焦点F作与x轴不垂直的任意直线l”交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则
为定值,且定值是
”.命题中涉及了这么几个要素:给定的圆锥曲线E,过该圆锥曲线焦点F的弦AB,AB的垂直平分线与焦点所在的对称轴的交点M,AB的长度与F、M两点间距离的比值.试类比上述命题,写出一个关于抛物线C的类似的正确命题,并加以证明
(Ⅲ)试推广(Ⅱ)中的命题,写出关于圆锥曲线(椭圆、双曲线、抛物线)的统一的一般性命题(不必证明).
查看习题详情和答案>>
| ||
| 3 |
(Ⅰ)求双曲线C的方程;
(Ⅱ)命题:“过椭圆
| x2 |
| 25 |
| y2 |
| 16 |
| |AB| |
| |FM| |
| 10 |
| 3 |
(Ⅲ)试推广(Ⅱ)中的命题,写出关于圆锥曲线(椭圆、双曲线、抛物线)的统一的一般性命题(不必证明).
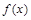 满足:①对任意的
满足:①对任意的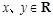 ,都有
,都有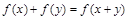 ;②当
;②当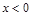 时,有
时,有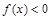 .
.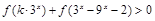 在
在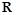 上有解,求实数
上有解,求实数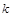 的取值范围.
的取值范围.