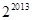摘要:若数列{}满足 则的值为 .
网址:http://m.1010jiajiao.com/timu3_id_502068[举报]
若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”.已知数列
为“平方递推数列”.已知数列 中,
中, ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中 为正整数.
为正整数.
(Ⅰ)证明数列 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列;
为等比数列;
(Ⅱ)设(Ⅰ)中“平方递推数列”的前 项积为
项积为 ,即
,即 ,求
,求 ;
;
(Ⅲ)在(Ⅱ)的条件下,记 ,求数列
,求数列 的前
的前 项和
项和 ,并求使
,并求使 的
的 的最小值.
的最小值.
查看习题详情和答案>>
若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”.已知数列
为“平方递推数列”.已知数列 中,
中, ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中 为正整数.
为正整数.
(Ⅰ)证明数列 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列;
为等比数列;
(Ⅱ)设(Ⅰ)中“平方递推数列”的前 项积为
项积为 ,即
,即 ,求
,求 ;
;
(Ⅲ)在(Ⅱ)的条件下,记 ,求数列
,求数列 的前
的前 项和
项和 ,并求使
,并求使 的
的 的最小值.
的最小值.
若数列![]() 满足:
满足:![]() 是常数),则称数列
是常数),则称数列![]() 为二阶线性递推数列,且定义方程
为二阶线性递推数列,且定义方程![]() 为数列
为数列![]() 的特征方程,方程的根称为特征根; 数列
的特征方程,方程的根称为特征根; 数列![]() 的通项公式
的通项公式![]() 均可用特征根求得:
均可用特征根求得:
①若方程![]() 有两相异实根
有两相异实根![]() ,则数列通项可以写成
,则数列通项可以写成![]() ,(其中
,(其中![]() 是待定常数);
是待定常数);
②若方程![]() 有两相同实根
有两相同实根![]() ,则数列通项可以写成
,则数列通项可以写成![]() ,(其中
,(其中![]() 是待定常数);
是待定常数);
再利用![]() 可求得
可求得![]() ,进而求得
,进而求得![]() .
.
根据上述结论求下列问题:
(1)当![]() ,
,![]() (
(![]() )时,求数列
)时,求数列![]() 的通项公式;
的通项公式;
(2)当![]() ,
,![]() (
(![]() )时,求数列
)时,求数列![]() 的通项公式;
的通项公式;
(3)当![]() ,
,![]() (
(![]() )时,记
)时,记![]() ,若
,若![]() 能被数
能被数![]() 整除,求所有满足条件的正整数
整除,求所有满足条件的正整数![]() 的取值集合.
的取值集合.
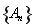

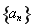
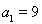
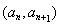
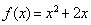
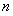

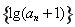
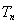
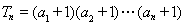
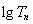
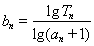
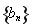
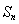
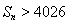
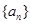 满足
满足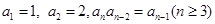 ,则
,则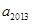 的值为 ( )
的值为 ( )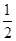 C.1 D.
C.1 D.