摘要：[ ]1已知:是R上的增函数.点.在它的图像上.为其反函数.则不等式＜1的解集是 (A), (B), (C), (D). [ ]2定义在R上的函数满足.当时..则当时.的最小值是(A),(B),(C),(D). [ ]3设曲线在处的切线方程为.则 (A),(B),(C),(D). [ ]4已知数列...--..--.它的前n项积大于.则正整数n的最小值为 11, (D)12. [ ]5集合..若只有一个子集.则实数k的取值范围为 (A), (B), (C), (D). [ ]6有4位学生参加某种竞赛.竞赛规则规定:每位同学必须从甲.乙两题中任选一题作答.选甲答对得100分.答错得分,选乙答对得90分.答错得分.若4位同学的总分为0分.则这4位同学不同得分情况的种数是 36, 18. [ ]7某班有48名学生.某次数学测验.算术平均分为70分.标准差为.后发现成绩记录有误.某甲得80分却记为50分.某乙得70分却记为100分.更正后计算得标准差为.则与之间大小关系是 (A)＞, (B), (C)＞, (D)＜. [ ]8四棱锥中...底面为梯形...满足上述条件的四棱锥的顶点的轨迹是不完整的圆, 抛物线的一部分. [ ]9已知实数且.则的取值范围为 (A), (B), (C), (D). [ ]10 若.则的最小值为 (A), (B), (C), (D).

网址：http://m.1010jiajiao.com/timu3_id_501679[举报]

+cx+d，x∈R（a，b，c，d为常数且a≠0），f'（x）=0是关于x的一元二次方程，根的判别式为△，给出下列四个结论：
①△＜0是y=f（x）在（-∞，+∞）为单调函数的充要条件；
②若x₁、x₂分别为y=f（x）的极小值点和极大值点，则x₂＞x₁；
③当a＞0，△=0时，f（x）在（-∞，+∞）上单调递增；
④当c=3，b=0，a∈（0，1）时，y=f（x）在[-1，1]上单调递减．
其中正确结论的序号是

．（填写你认为正确的所有结论序号）

查看习题详情和答案>>

已知定义在R上的函数f(x)对任意实数x₁、x₂满足关系：f(x₁＋x₂)＝f(x₁)＋f(x₂)＋2

(1)求f(0)的值；

(2)证明：f(x)的图象关于点(0，－2)成中心对称图形；

(3)若x＞0，则有f(x)＞－2，求证：f(x)在R上是增函数．

查看习题详情和答案>>

已知关于x的函数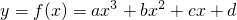 $数学公式$ ，x∈R（a，b，c，d为常数且a≠0），f'（x）=0是关于x的一元二次方程，根的判别式为△，给出下列四个结论：
①△＜0是y=f（x）在（-∞，+∞）为单调函数的充要条件；
②若x₁、x₂分别为y=f（x）的极小值点和极大值点，则x₂＞x₁；
③当a＞0，△=0时，f（x）在（-∞，+∞）上单调递增；
④当c=3，b=0，a∈（0，1）时，y=f（x）在[-1，1]上单调递减．
其中正确结论的序号是________．（填写你认为正确的所有结论序号）

查看习题详情和答案>>

解答题

已知f(x)是定义在实数集R上的增函数，设F(x)＝f(x)―f(a―x)．

(1)

求证：F(x)在R上是增函数；

(2)

求F的值，并证明y＝F(x)的图象关于点中心对称；

(3)

若对任意x、y∈R，满足F(x＋y)＋F(x－y)＝2F(x)F(y)，求证对任意x∈R，总有F(x＋a)＝－F(x)

查看习题详情和答案>>

下图展示了一个由区间（其中为一正实数)到实数集R上的映射过程：区间中的实数对应线段上的点，如图1；将线段围成一个离心率为的椭圆，使两端点、恰好重合于椭圆的一个短轴端点，如图2 ；再将这个椭圆放在平面直角坐标系中，使其中心在坐标原点，长轴在轴上，已知此时点的坐标为，如图3，在图形变化过程中，图1中线段的长度对应于图3中的椭圆弧ADM的长度.图3中直线与直线交于点，则与实数对应的实数就是，记作,