摘要:19. 设数列{an}满足a1 = 2.an +1 = 3an-2.n = 1.2.3.-. (I)求证:数列{an-1}是等比数列, (II)求{an}的通项公式, (III)求{an}的前n项和Sn. 解:(I)证明:∵ an +1 = 3an-2.且a1 = 2. ∴ an +1-1 = 3 (an-1).且an≠1. ∴ = 3.∴数列{an-1}是等比数列. (II)∵数列{an-1}是等比数列. ∴ an-1 = (a1-1)·qn-1 = (2-1)·3n-1 = 3n-1. ∴ an = 3n-1 + 1. ∴ {an}的通项公式an = 3n-1 + 1. (III)Sn = a1 + a2 + a3 + - + an = (30 + 1) + + (32 + 1) + - + (3n-1 + 1) = (30 + 3 + 32 + - + 3n-1 ) + n =+ n =×3n + n-.
网址:http://m.1010jiajiao.com/timu3_id_501654[举报]
(本小题满分14分)设数列{an}为前n项和为Sn,数列{bn}满足:bn =nan,且数列{bn}的前n项和为(n-1)Sn+2n (n∈N*).
(1)求a1,a2的值;
(2)求证:数列{ Sn +2}是等比数列;
(3)抽去数列{an}中的第1项,第4项,第7项,……,第3n-2项,余下的项顺序不变,组成一个新数列{cn},若{cn}的前n项和为Tn,求证:
<≤
查看习题详情和答案>> (本小题满分14分)设函数f (x)满足f (0) =1,且对任意![]() ,都有f (xy+1) = f (x) f (y)-f (y)-x+2.(I) 求f (x) 的解析式;(II) 若数列{an}满足:an+1=3f (an)-1(n ?? N*),且a1=1,求数列{an}的通项公式;
,都有f (xy+1) = f (x) f (y)-f (y)-x+2.(I) 求f (x) 的解析式;(II) 若数列{an}满足:an+1=3f (an)-1(n ?? N*),且a1=1,求数列{an}的通项公式;
(Ⅲ)求数列{an}的前n项和Sn.
查看习题详情和答案>>(本小题满分14分)
已知:有穷数列{an}共有2k项(整数k≥2 ),a1=2 ,设该数列的前n项和为 Sn且满足Sn+1=aSn+2(n=1,2,…,2k-1),a>1.
(1)求{an}的通项公式;
(2)设bn=log2an ,求{bn}的前n项和Tn;
(3)设cn=![]() ,若a=2
,若a=2![]() ,求满足不等式
,求满足不等式![]() +
+![]() +…+
+…+![]() +
+![]() ≥
≥![]() 时k的最小值.
时k的最小值.
 ,若a=2
,若a=2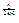 ,求满足不等式
,求满足不等式 +
+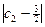 +…+
+…+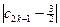 +
+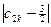 ≥
≥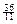 时k的最小值.
时k的最小值.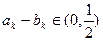 ?若存在,求出k,若不存在,说明理由.
?若存在,求出k,若不存在,说明理由.