摘要:22.抛物线的项点为 准线为----------- 设双曲线G为则有.可得.a2=3.b2=9. ∴双曲线G的方程为.-------- (2)①由.得------------ 又由.--- 设---------- ∵若原点O在AB为直径的圆上.有OA⊥OB.KOA·KOB=-1..即 -- 化简为 ---解得.. 故.当k=±1时.原点O在AB为直径的圆上.--- ②设这样的实数k存在.则有 -----① ------ -----② ------ -----③ ------ 由②③得.---------------- 即.推得km=3.-------------- 这与km=-1矛盾.所以适合条件的k不存在.---------
网址:http://m.1010jiajiao.com/timu3_id_501097[举报]
(08年岳阳一中二模文)(14分) 已知![]() 是抛物线
是抛物线![]() 的任一弦,
的任一弦,![]() 为抛物线的焦点,
为抛物线的焦点,![]() 为准线。
为准线。![]() 为过点
为过点![]() 且以向量
且以向量![]() 为方向向量的直线.
为方向向量的直线.
(1) 若过点![]() 的抛物线的切线与
的抛物线的切线与![]() 轴相交于点
轴相交于点![]() ,求证:
,求证:![]() ;
;
(2) 若![]() (
(![]() 异于原点),直线
异于原点),直线![]() 与
与![]() 相交于点
相交于点![]() ,求点
,求点![]() 的轨迹方程;
的轨迹方程;
(3) 若![]() 过焦点
过焦点![]() ,分别过
,分别过![]() 的抛物线的两切线相交于点
的抛物线的两切线相交于点![]() ,求证:
,求证:![]() ,且
,且![]() 在直线
在直线![]() 上。
上。
查看习题详情和答案>>
如图,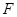 是抛物线
是抛物线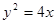 的焦点,
的焦点,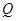 为准线与
为准线与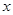 轴的交点,直线
轴的交点,直线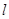 经过点
经过点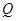 .
.
(Ⅰ)直线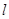 与抛物线有唯一公共点,求
与抛物线有唯一公共点,求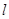 的方程;
的方程;
|
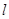 与抛物线交于
与抛物线交于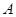 、
、 两点记
两点记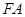 、
、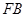 的斜率分别为
的斜率分别为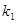 ,
,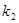 .
.
(1)求证: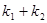 为定值;
为定值;
(2)若点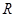 在线段
在线段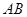 上,且满足
上,且满足
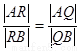 ,求点
,求点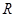 的轨迹方程.
的轨迹方程.
查看习题详情和答案>>
(本大题12分)
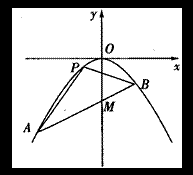 如图,抛物线的项点O在坐标原点,焦点在y轴负半轴上,过点M(0,-2)作直线
如图,抛物线的项点O在坐标原点,焦点在y轴负半轴上,过点M(0,-2)作直线![]() 与抛物线相交于A,B两点,且满足
与抛物线相交于A,B两点,且满足![]() (I)求直线
(I)求直线![]() 和抛物线的方程;
和抛物线的方程;
(II)当抛物线上一动点P从点A向点B运动时,求![]() 面积的最大值。
面积的最大值。
已知抛物线C以原点O为顶点,其准线方程为x=-1,焦点为F.
①求抛物线C的标准方程;
②过点P(-1,0)的直线l与抛物线C相交于A、B两点.
(ⅰ)证明:
•
为定值;
(ⅱ)点A关于x轴的对称点为D,证明:点F在直线BD上.
查看习题详情和答案>>
①求抛物线C的标准方程;
②过点P(-1,0)的直线l与抛物线C相交于A、B两点.
(ⅰ)证明:
| OA |
| OB |
(ⅱ)点A关于x轴的对称点为D,证明:点F在直线BD上.
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f′′(x)是函数y=f(x)的导函数y=f′(x)的导数,若f′′(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.现已知f(x)=x3-3x2+2x-2,请解答下列问题:
(Ⅰ)求函数f(x)的“拐点”A的坐标;
(Ⅱ)求证f(x)的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明);
(Ⅲ)若另一个三次函数G(x)的“拐点”为B(0,1),且一次项系数为0,当x1>0,x2>0(x1≠x2)时,试比较
与G(
)的大小.
查看习题详情和答案>>
(Ⅰ)求函数f(x)的“拐点”A的坐标;
(Ⅱ)求证f(x)的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明);
(Ⅲ)若另一个三次函数G(x)的“拐点”为B(0,1),且一次项系数为0,当x1>0,x2>0(x1≠x2)时,试比较
| G(x1)+G(x2) |
| 2 |
| x1+x2 |
| 2 |