摘要:(理)解关于x的不等式:.. (文)解关于x的不等式:.. 已知z1=3+4.z2=65 且 (Ⅰ)求, (Ⅱ)设z1.z2在复平面内所对应点分别为P.Q.O为坐标原点.以OP.OQ为边作 平行四边形OPRQ.求对角线OR的长及平行四边形OPRQ的面积. 如图.已知四棱锥P-ABCD的侧面PAD与底面ABCD垂直.△PAD是边长为a的正三角形.ABCD为直角梯形. AB//CD.DC=2a.∠ADC=90°.∠DCB=45°.E为BP中 点.F在PC上且PF=PC. (Ⅰ)求证EF//平面PAD, (Ⅱ)求三棱锥E-PCD的体积. (20)(本小题满分12分.文科做 已知奇函数 (Ⅰ)试确定实数a的值.并证明f(x)为R上的增函数, (Ⅱ)记求, (Ⅲ)若方程在上有解.试证. 某公司按现有能力.每月收入为70万元.公司分析部门测算.若不进行改革.入世后因竞争加剧收入将逐月减少.分析测算得入世第一个月收入将减少3万元.以后逐月多减少2万元.如果进行改革.即投入技术改造300万元.且入世后每月再投入1万元进行员工培训.则测算得自入世后第一个月起累计收入Tn与时间n的关系为Tn=an+b.且入世第一个月时收入将为90万元.第二个月时累计收入为170万元.问入世后经过几个月.该公司改革后的累计纯收入高于不改革时的累计纯收入. (22)(本小题满分14分.文科只做 已知抛物线C:的焦点为原点.C的准线与直线 的交点M在x轴上.与C交于不同的两点A.B.线段AB的垂直平分线交x轴于点N(p.0). (Ⅰ)求抛物线C的方程, (Ⅱ)求实数p的取值范围, (Ⅲ)若C的焦点和准线为椭圆Q的一个焦点和一条准线.试求Q的短轴的端点的轨迹方程.
网址:http://m.1010jiajiao.com/timu3_id_501045[举报]
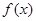 是R上的单调函数,且"x∈R,
是R上的单调函数,且"x∈R,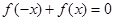 ,若
,若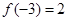
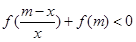 ,其中m∈R且m > 0
,其中m∈R且m > 0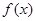 是R上的单调函数,且"x∈R,
是R上的单调函数,且"x∈R,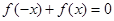 ,若
,若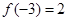
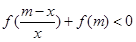 ,其中m∈R且m > 0
,其中m∈R且m > 0