摘要:解析: ①展开式的通项公式为Tr+1=(-1)r27-r(r=0,1,2),令21-r=0得r=6,即常数项为T7,∴①假. ②在△ABC中,A>Ba>b2RsinA>2RsinB>0sin2A>sin2B>cos2A<cos2B,②真. ③由抛物线y=f(x)=x2-x+a的对称性知点(m,f(m))和点(1-m,f(1-m))关于直线x=对称,∴f(1-m)=f(m)>0,③真. ④连结空间四边形ABCD的对角线AC·BD后,得棱锥A-BCD是棱长为a的正四面体,在侧面ABC内, 与的夹角为120°,∴2·=-a2,∴④假. 答案: ②③
网址:http://m.1010jiajiao.com/timu3_id_500715[举报]
已知 的展开式中第3项的系数与第5项的系数之比为
的展开式中第3项的系数与第5项的系数之比为 .
.
(1)求 的值;(2)求展开式中的常数项.
的值;(2)求展开式中的常数项.
【解析】(1)利用二项展开式的通项公式求出展开式的通项,求出展开式中第3项与第5项的系数列出方程求出n的值.
(2)将求出n的值代入通项,令x的指数为0求出r的值,将r的值代入通项求出展开式的常数项.
查看习题详情和答案>>
 的展开式中第3项与第7项的二项式系数相等,则该展开式中
的展开式中第3项与第7项的二项式系数相等,则该展开式中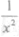 的系数为_________.
的系数为_________.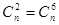 ,所以
,所以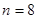 ,所以展开式的通项为
,所以展开式的通项为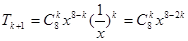 ,令
,令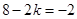 ,解得
,解得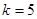 ,所以
,所以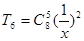 ,所以
,所以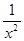 的系数为
的系数为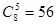 .
.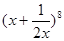 的展开式中
的展开式中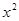 的系数为____________.
的系数为____________.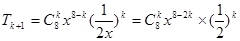 ,令
,令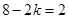 ,解得
,解得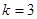 ,所以
,所以 ,所以
,所以