摘要：7．定义在区间上的奇函数f在区间[0.+∞)上的图象与f(x)的图象重合．设a＞b＞0.给出下列不等式: ①f, ②f, ③f, ④f． 其中成立的是 [ ] A．①与④ B．②与③ C．①与③ D．②与④ [ ] A．{x|0＜x＜2＝ B．{x|0＜x＜2.5}
网址：http://m.1010jiajiao.com/timu3_id_500642[举报]
已知函数f(x)＝logm
(1)判断f(x)的奇偶性并证明；
(2)若f(x)的定义域为[α，β](β＞α＞0)，判断f(x)在定义域上的增减性，并加以证明；
(3)若0＜m＜1，使f(x)的值域为[logmm(β－1)，logmm(α－1)]的定义域区间[α，β](β＞α＞0)是否存在？若存在，求出[α，β]，若不存在，请说明理由．
定义在区间（－∞，＋∞）上的奇函数f（x）为增函数；偶函数g（x）在区间
上的图像与f（x）的图像重合，设a＞b＞0，给出下列不等式
① f（b）－f（－a）＞g（a）－g（－b）
② f（b）－f（－a）＜g（a）－g（－b）
③ f（a）－f（－b）＞g（b）－g（－a）
④f（a）－f（－b）＜g（b）－g（－a）
其中，成立的是（ ）
|
(A) ①，④ |
(B) ②，③ |
(C) ①，③ |
(D) ②，④ |
定义在区间（－∞，＋∞）上的奇函数f（x）为增函数；偶函数g（x）在区间
上的图像与f（x）的图像重合，设a＞b＞0，给出下列不等式
查看习题详情和答案>>
上的图像与f（x）的图像重合，设a＞b＞0，给出下列不等式
① f（b）－f（－a）＞g（a）－g（－b）
② f（b）－f（－a）＜g（a）－g（－b）
③ f（a）－f（－b）＞g（b）－g（－a）
④f（a）－f（－b）＜g（b）－g（－a）
其中，成立的是（ ）
|
(A) ①，④ |
(B) ②，③ |
(C) ①，③ |
(D) ②，④ |
在定义域内是增函数；③函数
图象关于原点对称；④既是奇函数又是偶函数的函数一定是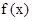
=0 
; ⑤函数y＝f(x＋2)图象与函数y＝f(2－x)图象关于直线x＝2对称；其中正确命题的个数为：（
）