摘要：17．解(I)+=(x,0)+(1,y)=(x+, y), –=(1,y)= (x,– y).(+)(), (+)·()=0, (x+)( x)+y·(y)=0, 故P点的轨迹方程为． (II)考虑方程组 消去y.得(1–3k2)x2-6kmx-3m2-3=0 (*) 显然1-3k20, =(6km)2-4(1-3k2)( -3m2-3)=12(m2+1-3k2)>0. 设x1,x2为方程*的两根.则x1+x2=.x0=, y0=kx0+m=, 故AB中点M的坐标为(.), 线段AB的垂直平分线方程为y=(), 将D坐标代入.化简得 4m=3k21, 故m.k满足 消去k2得 m24m>0, 解得 m<0或m>4. 又4m=3k21>1, 故m(,0)(4,+)．
网址：http://m.1010jiajiao.com/timu3_id_500039[举报]
设y=f（x）为定义在区间I上的函数，若对I上任意两个实数x1，x2都有f(
)≤
[f(x1)+f(x2)]成立，则f（x）称为I上的凹函数．
（1）判断f(x)=
(x＞0)是否为凹函数？
（2）已知函数f2（x）=x|ax-3|（a≠0）为区间[3，6]上的凹函数，请直接写出实数a的取值范围（不要求写出解题过程）；
（3）设定义在R上的函数f3（x）满足对于任意实数x，y都有f3（x+y）=f3（x）•f3（y）．求证：f3（x）为R上的凹函数．
查看习题详情和答案>>
| x1+x2 |
| 2 |
| 1 |
| 2 |
（1）判断f(x)=
| 3 |
| x |
（2）已知函数f2（x）=x|ax-3|（a≠0）为区间[3，6]上的凹函数，请直接写出实数a的取值范围（不要求写出解题过程）；
（3）设定义在R上的函数f3（x）满足对于任意实数x，y都有f3（x+y）=f3（x）•f3（y）．求证：f3（x）为R上的凹函数．
设y=f（x）为定义在区间I上的函数，若对I上任意两个实数x1，x2都有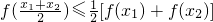
成立，则f（x）称为I上的凹函数．
（1）判断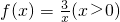
是否为凹函数？
（2）已知函数f2（x）=x|ax-3|（a≠0）为区间[3，6]上的凹函数，请直接写出实数a的取值范围（不要求写出解题过程）；
（3）设定义在R上的函数f3（x）满足对于任意实数x，y都有f3（x+y）=f3（x）•f3（y）．求证：f3（x）为R上的凹函数．
查看习题详情和答案>>
设y=f（x）为定义在区间I上的函数，若对I上任意两个实数x1，x2都有f(
)≤
[f(x1)+f(x2)]成立，则f（x）称为I上的凹函数．
（1）判断f(x)=
(x＞0)是否为凹函数？
（2）已知函数f2（x）=x|ax-3|（a≠0）为区间[3，6]上的凹函数，请直接写出实数a的取值范围（不要求写出解题过程）；
（3）设定义在R上的函数f3（x）满足对于任意实数x，y都有f3（x+y）=f3（x）•f3（y）．求证：f3（x）为R上的凹函数．
查看习题详情和答案>>
| x1+x2 |
| 2 |
| 1 |
| 2 |
（1）判断f(x)=
| 3 |
| x |
（2）已知函数f2（x）=x|ax-3|（a≠0）为区间[3，6]上的凹函数，请直接写出实数a的取值范围（不要求写出解题过程）；
（3）设定义在R上的函数f3（x）满足对于任意实数x，y都有f3（x+y）=f3（x）•f3（y）．求证：f3（x）为R上的凹函数．