摘要:14.已知数列{an}各项均为正数.Sn为其前n项的和.对于任意的.都有. I.求数列的通项公式. II.若对于任意的恒成立.求实数的最大值.
网址:http://m.1010jiajiao.com/timu3_id_500013[举报]
已知数列{an}各项均为正数,Sn为其前n项和,对于 ,总有
,总有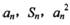 成等差数列.
成等差数列.
(I )求数列{an}的通项an;
(II )设数列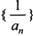 的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:
的前n项和为Tn,数列{Tn}的前n项和为Rn,求证: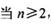
 时,
时,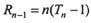 ;
;
(III)对任意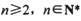 ,试比较
,试比较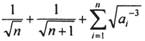 与
与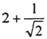 的大小
的大小
查看习题详情和答案>>
已知数列{an}各项均为正数,Sn为其前n项和,对于n∈N*,总有 成等差数列.
成等差数列.
(I)求数列{an}的通项an;
(II)设数列{ }的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:当n≥2,n∈N*时,Rn-1=n(Tn-1);
}的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:当n≥2,n∈N*时,Rn-1=n(Tn-1);
(III)对任意n≥2,n∈N*,试比较
 与2+
与2+ 的大小.
的大小.
查看习题详情和答案>>
 成等差数列.
成等差数列.(I)求数列{an}的通项an;
(II)设数列{
 }的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:当n≥2,n∈N*时,Rn-1=n(Tn-1);
}的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:当n≥2,n∈N*时,Rn-1=n(Tn-1);(III)对任意n≥2,n∈N*,试比较

 与2+
与2+ 的大小.
的大小.查看习题详情和答案>>
已知数列{an}各项均为正数,Sn为其前n项和,对于n∈N*,总有 成等差数列.
成等差数列.
(I)求数列{an}的通项an;
(II)设数列{ }的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:当n≥2,n∈N*时,Rn-1=n(Tn-1);
}的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:当n≥2,n∈N*时,Rn-1=n(Tn-1);
(III)对任意n≥2,n∈N*,试比较
 与2+
与2+ 的大小.
的大小.
查看习题详情和答案>>
 成等差数列.
成等差数列.(I)求数列{an}的通项an;
(II)设数列{
 }的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:当n≥2,n∈N*时,Rn-1=n(Tn-1);
}的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:当n≥2,n∈N*时,Rn-1=n(Tn-1);(III)对任意n≥2,n∈N*,试比较

 与2+
与2+ 的大小.
的大小.查看习题详情和答案>>