摘要：设F是椭圆的右焦点.P(x, y)是椭圆上一点.则|FP|等于( ). (A)ex+a (B)ex-a (C)ax-e (D)a-ex 提示:椭圆的定义:1.到两定点距离之和等于定值的点的轨迹,2.到定点和定直线距离之比等于定值的点的轨迹.
网址：http://m.1010jiajiao.com/timu3_id_499869[举报]
已知点F是椭圆
的右焦点，点M(m，0)、N(0，n)分别是x轴、y轴上的动点，且满足
．若点P满足
．
(Ⅰ)求点P的轨迹C的方程；
(Ⅱ)设过点F任作一直线与点P的轨迹交于A、B两点，直线OA、OB与直线x＝－a分别交于点S、T(O为坐标原点)，试判断
是否为定值？若是，求出这个定值；若不是，请说明理由．
设椭圆
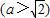的右焦点为F1，直线
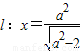与x轴交于点A，若
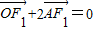（其中O为坐标原点）．
（1）求椭圆M的方程；
（2）设P是椭圆M上的任意一点，EF为圆N：x2+（y-2）2=1的任意一条直径（E、F为直径的两个端点），求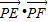
的最大值．
查看习题详情和答案>>
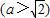的右焦点为F1，直线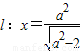与x轴交于点A，若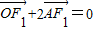（其中O为坐标原点）．（1）求椭圆M的方程；
（2）设P是椭圆M上的任意一点，EF为圆N：x2+（y-2）2=1的任意一条直径（E、F为直径的两个端点），求
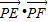的最大值．查看习题详情和答案>>
设椭圆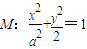
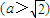的右焦点为F1，直线
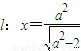与x轴交于点A，若
（其中O为坐标原点）．
（1）求椭圆M的方程；
（2）设P是椭圆M上的任意一点，EF为圆N：x2+（y-2）2=1的任意一条直径（E、F为直径的两个端点），求
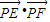的最大值．
查看习题详情和答案>>
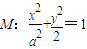
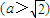的右焦点为F1，直线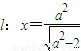与x轴交于点A，若（其中O为坐标原点）．（1）求椭圆M的方程；
（2）设P是椭圆M上的任意一点，EF为圆N：x2+（y-2）2=1的任意一条直径（E、F为直径的两个端点），求
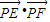的最大值．查看习题详情和答案>>
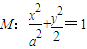
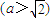的右焦点为F1，直线
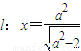与x轴交于点A，若
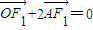（其中O为坐标原点）．
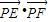的最大值．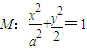
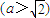的右焦点为F1，直线
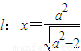与x轴交于点A，若
（其中O为坐标原点）．
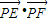的最大值．