摘要:给定一个圆锥和两个平面α.β.其中α∥β.且它们与圆锥底面平行.若平面α把圆锥侧面分成面积相等的两部分.平面β把圆锥分成体积相等的两部分.求夹在α.β间的几何体的体积与圆锥体积之比. 分析:本题涉及到截锥性质:截面积与底面积的比为对应元素的平方比.截得的圆锥的体积与原圆锥的体积之比是对应元素的立方比. 解:设给定圆锥的底面半径为R.高为H.则V圆锥=πR2H, 设平面α.β与圆锥侧面相交所得两圆半径分别为r1和r2. 由截锥性质得: 显然r2>r1.即平面β比平面α离圆锥底面近些.又设截得的两圆锥的高分别是h1和h2.则夹在α.β间的圆台的高h.有: h= h2-h1=, V圆台=π××() =×πR2H ∴V圆台:V圆锥=
网址:http://m.1010jiajiao.com/timu3_id_499380[举报]
如图2-3-9,正方体有8个顶点和12条棱,每条棱上均有一个中点,于是有棱的中点12个,顶点与中点合起来共有20个〔图2-3-9(1)〕.过其中的两点可作一条直线;过其中不在同一直线上的三点可作一个平面.现在考虑这些直线与平面的垂直关系.
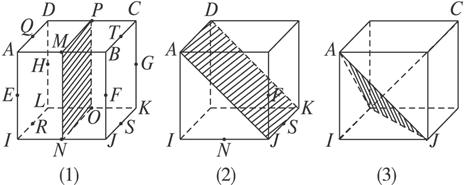
图2-3-9
(1)试举出一直线与一平面相互垂直的例子(不少于4例).
(2)若一直线与一平面相互垂直,我们就说这条直线与这个平面构成了一个“垂直关系组”,两个“垂直关系组”当且仅当其中两条直线和两个平面不全同一时称为相异的(或不同的).试求与正方体的棱相关的“垂直关系组”的个数.
查看习题详情和答案>>
如图,正方体有8个顶点和12条棱,每条棱上均有一个中点,于是有棱的中点12个,顶点与中点合起来共有20个〔图 (1)〕.过其中的两点可作一条直线;过其中不在同一直线上的三点可作一个平面.现在考虑这些直线与平面的垂直关系.
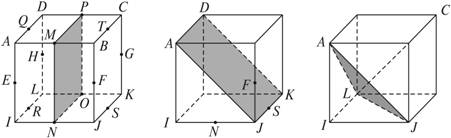
(1)试举出一直线与一平面相互垂直的例子(不少于4例);
(2)若一直线与一平面相互垂直,我们就说这条直线与这个平面构成了一个“垂直关系组”,两个“垂直关系组”当且仅当其中两条直线和两个平面不全同一时称为相异的(或不同的).试求与正方体的棱相关的“垂直关系组”的个数.
查看习题详情和答案>>下列命题中,不正确的是( ).
A.一直线和两个平面a 、b 所成的角相等,那么a ∥b
B.平面a ∥平面b ,则a 内的任意直线平行于平面b
C.一个三角形有两条边所在直线平行一个平面,那么三角形所在平面与这个平面平行
D.分别在两个平行平面内的两条直线只能是平行直线或异面直线
查看习题详情和答案>>