摘要：2．解:由已知------------------2分 由----4分 ∴当a≠0时.{an} 从第二项起成等比数列. 若{an}是等比数列.则首项为a.公比为2. ∴2a+b=a ∴a+b=0--------------------6分 ∴若{an}为等比数列.a.b应满足的条件是a+b=0.且a.b均不为零.-8分 ----------10分 -------12分 3． 长方体ABCD-A1B1C1D1中.AB=BC=1.AA1=2.E 是侧棱BB1中点. (Ⅰ)求证:直线AE⊥平面A1D1E, (Ⅱ)求二面角E-AD1-A1的大小, (Ⅲ)求三棱锥A-C1D1E的体积. 解:(Ⅰ)已知几何体为长方体 ∴A1D1⊥平面ABB1A1 ∴A1D1⊥AE------------2分 又AB＝1.BB1=2.E为BB1的中点 ∴△ABE为等腰直角三角形 ∴AE=同理A1E= ∴∠AEA1为直角 即AE⊥A1E ∴AE⊥平面A1D1E------------4分 (Ⅱ)取AA1中点O.连OE.则EO⊥A1A.EO⊥A1D1. ∴EO⊥平面ADD1A1----------------5分 过O在平面ADD1A1中作OF⊥AD1.交AD1于F 连结EF.则AD1⊥EF ∴∠EFO为二面角E-AD1-A1的平面角--------7分 即二面角------------9分 (Ⅲ)由于AB∥C1D1 ∴AB∥平面C1D1E -------12分 高考数学中档题精选(5)
网址：http://m.1010jiajiao.com/timu3_id_499073[举报]
已知函数f（x）=2x-m（m∈R），g(x)=ax2+
ax+1（a∈R），h（x）=2|x-a|
（Ⅰ）设A：存在实数x使得f（x）≤0（m∈R）成立；B：当a=-2时，不等式g（x）＞0有解．若“A”是“B”的必要不充分条件，求实数m的取值范围；
（Ⅱ）设C：函数y=h（x）在区间（4，+∞）上单调递增；D：?x∈R，不等式g（x）＞0恒成立．请问，是否存在实数a使“非C”为真命题且“C∨D”也为真命题？若存在，请求实数a的取值范围；若不存在，请说明理由．
查看习题详情和答案>>
| 1 | 2 |
（Ⅰ）设A：存在实数x使得f（x）≤0（m∈R）成立；B：当a=-2时，不等式g（x）＞0有解．若“A”是“B”的必要不充分条件，求实数m的取值范围；
（Ⅱ）设C：函数y=h（x）在区间（4，+∞）上单调递增；D：?x∈R，不等式g（x）＞0恒成立．请问，是否存在实数a使“非C”为真命题且“C∨D”也为真命题？若存在，请求实数a的取值范围；若不存在，请说明理由．
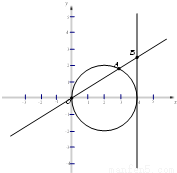
已知动直线y=kx交圆（x-2）2+y2=4于坐标原点O和点A，交直线x=4于点B，若动点M满足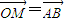
，动点M的轨迹C的方程为F（x，y）=0．
（1）试用k表示点A、点B的坐标；
（2）求动点M的轨迹方程F（x，y）=0；
（3）以下给出曲线C的五个方面的性质，请你选择其中的三个方面进行研究，并说明理由（若你研究的方面多于三个，我们将只对试卷解答中的前三项予以评分）．
①对称性；（2分）
②顶点坐标（定义：曲线与其对称轴的交点称为该曲线的顶点）；（2分）
③图形范围；（2分）
④渐近线；（3分）
⑤对方程F（x，y）=0，当y≥0时，函数y=f（x）的单调性．（3分）
查看习题详情和答案>>
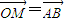，动点M的轨迹C的方程为F（x，y）=0．（1）试用k表示点A、点B的坐标；
（2）求动点M的轨迹方程F（x，y）=0；
（3）以下给出曲线C的五个方面的性质，请你选择其中的三个方面进行研究，并说明理由（若你研究的方面多于三个，我们将只对试卷解答中的前三项予以评分）．
①对称性；（2分）
②顶点坐标（定义：曲线与其对称轴的交点称为该曲线的顶点）；（2分）
③图形范围；（2分）
④渐近线；（3分）
⑤对方程F（x，y）=0，当y≥0时，函数y=f（x）的单调性．（3分）
查看习题详情和答案>>
已知函数f（x）=2x-m（m∈R），g(x)=ax2+
ax+1（a∈R），h（x）=2|x-a|
（Ⅰ）设A：存在实数x使得f（x）≤0（m∈R）成立；B：当a=-2时，不等式g（x）＞0有解．若“A”是“B”的必要不充分条件，求实数m的取值范围；
（Ⅱ）设C：函数y=h（x）在区间（4，+∞）上单调递增；D：?x∈R，不等式g（x）＞0恒成立．请问，是否存在实数a使“非C”为真命题且“C∨D”也为真命题？若存在，请求实数a的取值范围；若不存在，请说明理由．
查看习题详情和答案>>
| 1 |
| 2 |
（Ⅰ）设A：存在实数x使得f（x）≤0（m∈R）成立；B：当a=-2时，不等式g（x）＞0有解．若“A”是“B”的必要不充分条件，求实数m的取值范围；
（Ⅱ）设C：函数y=h（x）在区间（4，+∞）上单调递增；D：?x∈R，不等式g（x）＞0恒成立．请问，是否存在实数a使“非C”为真命题且“C∨D”也为真命题？若存在，请求实数a的取值范围；若不存在，请说明理由．
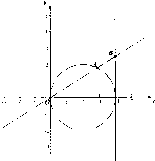已知点A（x1，y1）在圆（x-2）2+y2=4上运动，点A不与（0，0）重合，点B（4，y0）在直线x=4上运动，动点M（x，y）满足| OM |
| OB |
| OM |
| AB |
（1）试用点M的坐标x，y表示y0，x1，y1；
（2）求动点M的轨迹方程F（x，y）=0；
（3）以下给出曲线C的五个方面的性质，请你选择其中的三个方面进行研究，并说明理由．（若你研究的方面多于三个，我们将只对试卷解答中的前三项予以评分）
①对称性；
②顶点坐标（定义：曲线与其对称轴的交点称为该曲线的顶点）；
③图形范围；
④渐近线；
⑤对方程F（x，y）=0，当y≥0时，函数y=f（x）的单调性． 查看习题详情和答案>>
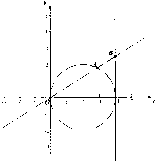已知点A（x1，y1）在圆（x-2）2+y2=4上运动，点A不与（0，0）重合，点B（4，y0）在直线x=4上运动，动点M（x，y）满足
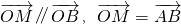．动点M的轨迹C的方程为F（x，y）=0．